Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 57
Encontre uma fórmula para a função descrita e obtenha seu domínio:
Um retângulo tem um perímetro de metros. Expresse a área do retângulo como uma função do comprimento de um de seus lados.
Passo 1
Eaee, belezinha??
Bom... a questão quer que encontremos a fórmula da área de um retângulo em função do comprimento de um de seus lados.
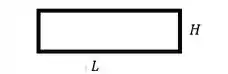
A área de um retângulo de lados e é dada por:
Essa é uma função que depende de duas variáveis ( e ). Para reduzi-la a apenas uma variável a questão nos diz que o perímetro do retângulo é de metros.
E o perímetro de um retângulo é dado pela soma dos lados:
Ah, a questão também quer que encontremos o domínio da função que a gente encontrar!
O domínio de uma função é o conjunto de valores possíveis para a variável de entrada da função, que nesse caso é o comprimento de um dos lados do retângulo.
Passo 2
Precisamos escrever um lado em função do outro. Podemos fazer isso a partir da expressão do perímetro!
O perímetro de metros é dado por:
Logo,
E podemos deixar em função de , tendo:
Agora, vamos conseguir reduzir a nossa função área para uma única variável.
Passo 3
Agora só substituímos a última expressão encontrada na expressão da área. Saca só:
Agora, sobre o domínio dessa função, precisamos que a nossa área seja positiva (afinal não existe área negativa) e também precisamos que o lado seja maior do que zero.
Olhando para a expressão da área fatorada, temos:
Para a área ser positiva, é preciso que ambos os fatores e sejam positivos ou ambos negativos.
No entanto, precisa ser positivo, pois não existe lado negativo.
Dessa forma, para a área ser positiva é preciso que e sejam positivos.
Ou seja, precisa ser menor que também.
Portanto, o domínio da nossa funç��o é:
Valores de maiores que resultam numa área negativa, e valores de menores que resultam num lado negativo, e nada disso existe num retângulo de verdade né!
Entendeu tudo? Responde Aí! 😉
