Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 4.Exercícios - Ex. 59

Sabendo que cos (pi)/(3) = (1)/(2) , qual é o valor de cos (2 pi)/(3) , cos (4 pi)/(3) e cos (5 pi)/(3) ?

Passo 1

Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!

Para resolver este exercício usaremos a simetria no ciclo trigonométrico, assim:

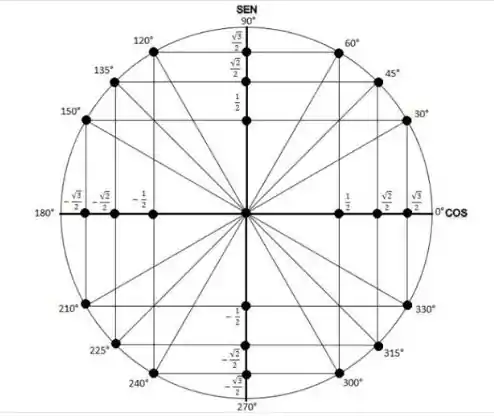
Passo 2

Desse modo, temos:

cos (pi)/(3) = cos (5 pi)/(3) = (1)/(2)

E

cos (2 pi)/(3) = cos (4 pi)/(3) = - (1)/(2)

Prontinho! Resolvido.

Resposta

cos (5 pi)/(3) = (1)/(2)

e

cos (2 pi)/(3) = cos (4 pi)/(3) = - (1)/(2)

Exercícios de Livros Relacionados

Um avião está a 7000 m de altura e inicia a aterrissagem (aeroporto ao nível do mar) em linha reta sob um ângulo de 6° com o solo. A que distância o avião está da cabeceira da pista? Qual distância o
Se s e nx + cos ⁡ x = a e s e nx∙ cos ⁡ x = b , obtenha uma relação entre a e b , independente de x.
Sabendo que s e n x + c o s x = a (a dado), calcule y = s e n^3 x + c o s^3 x .
Calcule s e n (pi)/(8) , c o s (pi)/(8) e t g (pi)/(8) .
Determine A nn B , sabendo que:A = {x = s e n (k pi)/(6) | k = 0,1 , ... , 12} B = {x = c o s (k pi)/(4) | k = 0,1 , ... , 8}