Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 2.Exercícios - Ex. 24
Um avião está a 7000 m de altura e inicia a aterrissagem (aeroporto ao nível do mar) em linha reta sob um ângulo de 6° com o solo. A que distância o avião está da cabeceira da pista? Qual distância o avião vai percorrer?
Passo 1
E aí pessoal, beleza?
Seguinte, como o avião está descendo de 7000 metros de altura numa linha reta que forma com o solo, temos a seguinte situação:
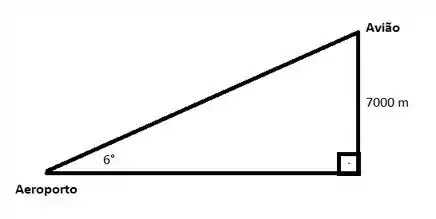
Então vamos usar a tangente para calcular a distância horizontal, beleza? Vamos chama-la de d.
Passo 2
Pela tabela da página 309, a tangente de é 0,10510, assim temos:
Passo 3
Show! Agora só falta calcular a distância que o avião vai percorrer.
Iiiih, como fazer isso?
PITÁÁÁÁGORAS! :D
Bora lá, vamos chamar essa distância de D e colocar as distâncias em km para facilitar:
Fechou! Vamos pra próxima?
Resposta
Exercícios de Livros Relacionados
Calcule:(s e n (pi - x) - c o s ((pi)/(2) - x) - t g (2 pi - x))/(t g (pi - x) - c o s (2 pi - x) + s e n ((pi)/(2) - x))
Calcule:a)[s e n x + cos ((pi)/(2) - x) [c o t g (x - pi) - c o t g (2 pi - x)]] b)(t g (x - pi) + s e c (pi - x))/([c o t g ((pi)/(2) - x) - c o s s e c (2 pi - x)] * c o s ((pi)/(2) - x))
Sabendo que s e n x = (1)/(2) e 0 = x = (pi)/(2) , calcule:a) cos x b) cos (x + (pi)/(2)) c) s e n (x + (pi)/(2)) d) t g (x + (pi)/(2)) e) c o t g (x + (pi)/(2)) f) sec (x + (pi)/(2)) g) c o s s e c (
Reduza ao 1° quadrante:a) cos 178 ° b) c o t g7 π 6 c) s e n7 π 6 d) s e n5 π 4 e) s e n251 ° f) sec 124 ° g) cos 5 π 3 h) cos 7 π 6 i) t g290 ° j) c o s s e c11 π 6 k) t g3 π 4 l) t g5 π 3
Reduza ao intervalo 0 , π 4 :a) s e n261 ° b) s e n4 π 3 c) s e n5 π 6 d) s e n5 π 3 e) cos 341 ° f) cos 2 π 3 g) cos 7 π 6 h) cos 4 π 3 i) t g151 ° j) t g5 π 3 k) t g11 π 6 l) t g2 π 3