Sabe-se que uma função contínua é negativa em e positiva em Por que a equação tem pelo menos uma solução entre e ? Exemplifique com um esboço.
Passo 1
Pelo Teorema do Valor Intermediário, se o limite entre dois valores diferentes numa mesma função apresentarem sinais diferentes, isso nos diz que existe pelo menos uma raiz nesse intervalo, certo?
Isso significa que, se a função do enunciado é negativa em e positiva em , existirá então pelo menos uma solução nesse intervalo.
Passo 2
Atenção no esboço.
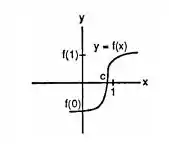
Independente do ponto onde a função cruza o eixo x, uma coisa é certa, pra passar de f(0) para f(1) em algum momento ele terá de cruzar.
Resposta
Ei, a resposta está no passo a passo :)