Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.5 - Ex. 52
(a) Demonstre que a equação tem pelo menos uma raiz real.
(b) Use sua calculadora para encontrar um intervalo de comprimento que contenha a raiz.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação:
Queremos provar através do Teorema do Valor Intermediário que existe uma raiz real dessa equação.
Para ficar melhor de a gente entender, a gente pode transformar essa equação em uma função (você vai já entender o porquê):
Mas o que diz esse Teorema?? Bom... diz o seguinte:
“Se for contínua em um intervalo fechado , e seja um número qualquer entre e , em que . Então existe um número em tal que ”.
Confuso né???
Em termos simples, vamos pegar o intervalo e substituir na nossa função.
Em seguida, vamos verificar se o zero da função (que é uma raiz) está de acordo com o intervalo dado.
Pelo Teorema do Valor intermediário, devemos ter o seguinte:
Ou
Agora bora lá!! 😉
Passo 2
A função é contínua no intervalo por ser um polinômio.
Substituindo os valores do intervalo, temos:
Agora, para , temos:
Como , então, pelo Teorema do Valor Intermediário, no intervalo há um número tal que , como queremos provar.
Passo 3
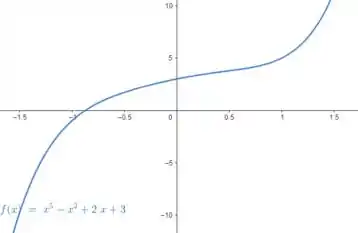
Plotando a função, temos:
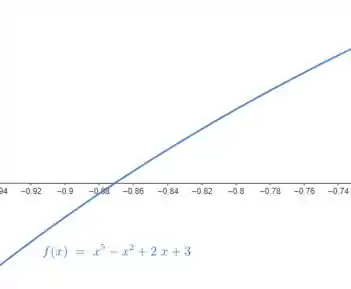
Aplicando um intervalo de , podemos verificar melhor a raiz:
Perceba que a raiz está contida no intervalo .
Resposta
Como , então, pelo Teorema do Valor Intermediário, no intervalo há um número tal que .
Dessa forma, existe uma raiz de no intervalo que é o nosso intervalo que contém a raiz.
