Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 52
São dados uma função f e os números n, a e b. Aproxime até quatro casas decimais a área da região limitada pela curva , pelo eixo x e as retas e fazendo o seguinte: divida o intervalo [a, b] em n subintervalos de unidades de largura.
, , , , retângulos circunscritos.
Passo 1
A questão nos pede para calcular a área cinza, limitada pelas três curvas e o eixo x:
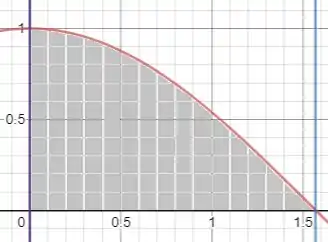
Devemos então, conforme pedido, utilizar retângulos circunscritos na região para realizar o cálculo.
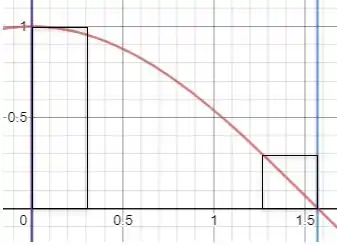
Passo 2
Como a nossa curva é decrescente no intervalo dado, , o valor máximo absoluto está no canto esquerdo dos subintervalos. Ou seja, usaremos para os nossos cálculos.
Temos que:
Sendo que:
Isto é, cada um dos 6 retângulos circunscritos possui de largura.
Passo 3
Podemos então calcular cada um dos que serão utilizados no cálculo, e também seus correspondentes.
Não esqueça de passar a sua calculadora para radiano! 😉
Podemos então calcular a área desejada:
Resposta
Obtemos então a área calculada da região sob o gráfico!