Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 36

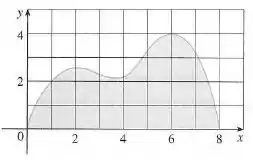
Utilize a Regra de Simpson para calcular o centroide da região dada.

Passo 1

Bom galera, nessa questão queremos encontrar o centroide da região. Para isso, utilizaremos a Regra de Simpson.

Passo 2

Utilizando n = 8 , temos

∆ x = b - a n = 8 - 0 8 = 1

Podemos então utilizando a regra do ponto médio encontrar a área, que é dada por

A = ∫ 0 8 f x d x = 1 3 f 0 + 4 f 1 + 2 f 2 + 4 f 3 + 2 f 4 + 4 f 5 + 2 f 6 + 4 f 7 + f 8 = 1 3 0 + 4 2.0 + 2 2.6 + 4 2.3 + 2 2.2 + 4 3.3 + 2 4.0 + 4 3.2 + 0

A = 20.26

Passo 3

Podemos calcular as coordenadas do centroide da seguinte maneira

M x = ∫ 0 8 x f x d x = 1 3 0 f 0 + 4 1 f 1 + 2 2 f 2 + 4 3 f 3 + 2 4 f 4 + 4 5 f 5 + 2 6 f 6 + 4 7 f 7 + 8 f 8 = 1 3 0 + 4 1 2.0 + 2 2 2.6 + 4 3 2.3 + 2 4 2.2 + 4 5 3.3 + 2 6 4.0 + 4 7 3.2 + 0 8 = 89.06

x - = 1 A ∫ 0 8 x f x d x = 4.39

M y = ∫ 0 8 f x 2 d x = 1 3 f 0 2 + 4 f 1 2 + 2 f 2 2 + 4 f 3 2 + 2 f 4 2 + 4 f 5 2 + 2 f 6 2 + 4 f 7 2 + f 8 2 = 1 3 0 + 4 2.0 2 + 2 2.6 2 + 4 2.3 2 + 2 2.2 2 + 4 3.3 2 + 2 4.0 2 + 4 3.2 2 + 0 = 58.96

y - = 1 A ∫ 0 8 f x 2 d x = 1.45

Resposta

x - ,   y - = 4.4 ,   1.5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x
O gráfico de y = 4 - | x | e o eixo x de x = - 4 até x = 4 formam um triângulo. Use o método desta secção para encontrar sua área.