Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 22
As massas pontuais estão localizadas no eixo conforme mostra a figura a seguir. Ache o momento do sistema com relação à origem e o centro de massa .
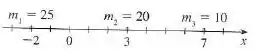
Passo 1
Bom galera, nesse exercício queremos encontrar o momento do sistema e seu centro de massa com base nas aplicações estudadas. Para isso, utilizaremos as aplicações da integração na física.
Passo 2
Para encontrar o momento , podemos utilizar a seguinte definição
Dessa forma, temos
Passo 3
Podemos encontrar o centro de massa utilizando a seguinte definição
Onde é a massa total do sistema. Dessa forma, temos
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a