Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 40
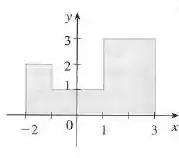
Encontre o centroide da região mostrada, não por integração, mas por localização dos centroides dos retângulos e triângulos (do Exercício ) e usando a aditividade dos momentos.
Passo 1
Bom galera, nesse exercício queremos encontrar o centroide da região mostrada sem utilizar a integração, mas sim utilizando a aditividade dos momentos.
Passo 2
O retângulo a esquerda do eixo possui centroide possui de área. Ao lado direito do eixo possui centroide e área .
Passo 3
Utilizando a aditividade dos momentos, temos
Resposta
O centroide é .
Exercícios de Livros Relacionados
São dados uma função f e os números n, a e b. Aproxime até quatro casas decimais a área da região limitada pela curva y = f x , pelo eixo x e as retas x = a e x = b fazendo o seguinte: divida o interv
São dados uma função f e os números n, a e b. Aproxime até quatro casas decimais a área da região limitada pela curva y = f x , pelo eixo x e as retas x = a e x = b fazendo o seguinte: divida o interv
São dados uma função f e os números n, a e b. Aproxime até quatro casas decimais a área da região limitada pela curva y = f x , pelo eixo x e as retas x = a e x = b fazendo o seguinte: divida o interv
São dados uma função f e os números n, a e b. Aproxime até quatro casas decimais a área da região limitada pela curva y = f x , pelo eixo x e as retas x = a e x = b fazendo o seguinte: divida o interv
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 1