Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios adicionais e avançados - Ex. 4
Um segmento de reta de comprimento a + b vai do eixo x ao eixo y. O ponto P no segmento está a unidades a partir de uma extremidade e b unidades a partir da outra extremidade. Mostre que P traça uma elipse conforme as extremidades do segmento deslizam ao longo dos eixos.
Passo 1
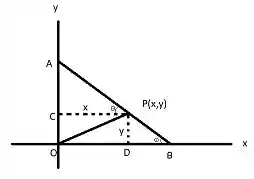Fala minha galera querida!! Vamos desenhar para ficar mais claro!
Pela semelhança de triângulos, ACP e PDB, podemos notar que os ângulo e, P e em B são iguais a , pois estão no mesmo segmento do de reta AB e em segmentos paralelos, CP e OB.
Passo 2
Temos então que,
e
Da relação fundamental da trigonometria,
Substituindo,
Que é a equação de uma elipse. Portanto P, traça uma elipse.
Bora pro próximo.
Resposta
Demonstração
Exercícios de Livros Relacionados
Seja P x 1 , y 1 um ponto na hipérbole x 2 a 2 - y 2 b 2 = 1 com focos F 1 e F 2 e sejam α e β os ângulos entre as retas P F 1,P F 2 e a hipérbole, como mostrado na figura. Demonstre que α = β . (Essa
Quais pontos no plano x y satisfazem as equações e desigualdades nos Exercícios 11-16? Desenhe uma figura para cada exercício. x 2 9 + y 2 16 ≤ 1
Quais pontos no plano x y satisfazem as equações e desigualdades nos Exercícios 11-16? Desenhe uma figura para cada exercício. 9 x 2 + 4 y 2 - 36 4 x 2 + 9 y 2 - 16 ≤ 0
Encontre uma equação para a curva traçada pelo ponto P(x, y) se a distância entre P e o vértice da parábola x 2 = 4 y for duas vezes a distância entre P e o foco. Identifique a curva.