Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 66

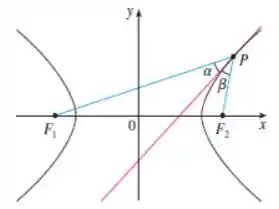
Seja P x 1 , y 1 um ponto na hipérbole x 2 a 2 - y 2 b 2 = 1 com focos F 1 e F 2 e sejam α e β os ângulos entre as retas P F 1   ,   P F 2 e a hipérbole, como mostrado na figura. Demonstre que α = β . (Essa é a propriedade de reflexão da hipérbole. Isso mostra que a luz dirigida ao foco F 2 de um espelho hiperbólico é refletida em direção ao outro foco F 1 .)

Passo 1

Beleza, pessoal? Nesse problema a gente tem uma hipérbole, e vamos provar que os ângulos α e β representados na figura são iguais.

O ângulo α   é o ângulo que está entre a reta que passa pelos pontos P e F 1 (vamos dizer que tem inclinação m 1 ) e a reta tangente à hipérbole, cuja inclinação m é a derivada nesse ponto P . E β é o ângulo que está entre a reta que passa pelos pontos P e F 2   (inclinação m 2 ) e a reta tangente à hipérbole.

m 2

m 1

Ele nos dá a dica de provar que as tangentes dos ângulos são iguais. E já que vamos trabalhar com tangentes, por que não trabalhar com as inclinações de cada reta que delimita os ângulos? Bora!

Passo 2

Pra calcular m 1 e m 2 , vamos usar Δ y Δ x , ok? Lembrando que as coordenadas do ponto P são ( x 1 , y 1 ) e dos focos são ( ± c , 0 ) .

m 1 = y 1 - 0 x 1 - - c

m 1 = y 1 x 1 + c

m 2 = y 1 - 0 x 1 - c

m 2 = y 1 x 1 - c

Agora, pra calcular m , vamos derivar a equação da hipérbole. Não se esqueça da regra da cadeia pra derivar termos envolvendo y , ok?

x 2 a 2 - y 2 b 2 = 1

1 a 2   2 x - 1 b 2   2 y   d y d x = 0

2 y b 2   d y d x = 2 x a 2

d y d x = b 2 x a 2 y

Para o ponto P , temos:

m = b 2 x 1 a 2 y 1

Passo 3

Show! Agora que temos as inclinações de cada reta, podemos a fórmula pra calcular a tangente do ângulo entre duas retas. Como α é o ângulo entre a reta P F 1 e a reta tangente à hipérbole, temos:

t g   α = m 1 - m 1 + m 1 m

t g   α = y 1 x 1 + c - b 2 x 1 a 2 y 1 1 + y 1 x 1 + c b 2 x 1 a 2 y 1

t g   α = a 2 y 1 2 - b 2 x 1 x 1 + c a 2 y 1 x 1 + c + b 2 x 1 y 1

t g   α = a 2 y 1 2 - b 2 x 1 2 - b 2 c x 1 ( a 2 + b 2 ) x 1 y 1 + a 2 c y 1

Pela equação da hipérbole, temos:

a 2 y 1 2 - b 2 x 1 2 = - a 2 b 2         e         a 2 + b 2 = c 2

Então,

t g   α = - a 2 b 2 - b 2 c x 1 c 2 x 1 y 1 + a 2 c y 1

t g   α = - b 2 a 2 + c x 1 c y 1 c x 1 + a 2

t g   α = - b 2 c y 1

t g   α = b 2 c y 1

Passo 4

Beleza! Agora fazemos os cálculos para β , que é o ângulo entre a reta P F 2 e a reta tangente à hiperbole

:

t g   β = m 2 - m 1 + m 2 m

t g   β = y 1 x 1 - c - b 2 x 1 a 2 y 1 1 + y 1 x 1 - c b 2 x 1 a 2 y 1

t g   β = a 2 y 1 2 - b 2 x 1 x 1 - c a 2 y 1 x 1 - c + b 2 x 1 y 1

t g   β = a 2 y 1 2 - b 2 x 1 2 + b 2 c x 1 a 2 + b 2 x 1 y 1 - a 2 c y 1

t g   β = - a 2 b 2 + b 2 c x 1 c 2 x 1 y 1 - a 2 c y 1

t g   β = b 2 c x 1 - a 2 c y 1 c x 1 - a 2

t g   β = b 2 c y 1

Então concluímos que t g   α = t g   β ,   e portanto, α = β , beleza?

Resposta

Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O planeta Mercúrio percorre uma órbita elíptica com excentricidade 0,206 . Sua distância mínima ao Sol é 4,6.10 7k m . Encontre sua distância máxima do Sol.
A distância do planeta Plutão até o Sol é 4,43.10 9k m no periélio e 7,37.10 9k m no afélio. Encontre a excentricidade da órbita de Plutão.
Esboce a curva com a equação dada. r = 1 - 3 cos ⁡ θ
Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico. x = 2 y 2
Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico.5. x + 2 2 = 8 ( y - 3 )