Seja a função definida pelo gráfico:

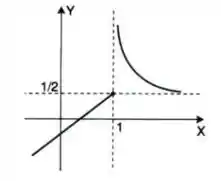
Intuitivamente, encontre se existir:

d)

Então pessoal, o que o enunciado quer é que observemos o gráfico e tentemos concluir se há algum valor para o qual a função tende quando é MUITO GRANDE positivamente! Se observarmos o gráfico, poderemos notar que quanto mais aumenta, mais vai se aproximando da assíntota horizontal que existe em . Para facilitar nossa visualização vamos desenhar algumas setas aqui, saca só:

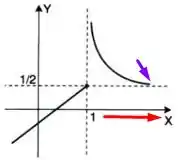
A seta vermelha se trata do sentido em que os números estão aumentando e a seta em roxo foi esboçada para indicar que a curva está TENDENDO a , é por isso que há essa reta pontilhada. A reta pontilhada quer dizer que a função irá se aproximar dela, mas nunca passará ou tocará essa reta.

Dessa forma, para um infinito, ou melhor, MUITO GRANDE, o resultado do limite será:

E esse é o nosso resultado!