Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.9 - Ex. 18

Seja F → x , y , z = z t g - 1 y 2 i → + z 3 ln ⁡ x 2 + 1 j → + z k → . Determine o fluxo de F → através da parte do paraboloide x 2 + y 2 + z = 2 que está acima do plano z = 1 e está orientada para baixo.

Passo 1

Oi galera, tudo bem? Vamos ver o que a questão quer!

Ela diz que existe um campo vetorial

F → x , y , z = z t g - 1 y 2 i → + z 3 ln ⁡ x 2 + 1 j → + z k →

E quer que determinemos o fluxo dele através da parte do paraboloide

x 2 + y 2 + z = 2

Que está acima do plano

z = 1

E está orientado para baixo.

Tudo certo?

O fluxo Φ é calculado assim:

Φ = ∭ V ∇ ⋅ F → d V

Lembrando que o divergente é calculado desse jeito para 3 coordenadas:

∇ ⋅ F → = ∂ ∂ x F x + ∂ ∂ y F y + ∂ ∂ z F z

Portanto, primeiro vamos esboçar esse gráfico, depois vamos ter que calcular esse divergente, depois montar a integral tripla em coordenadas cilíndricas, pois temos um paraboloide e isso facilita bastante e finalmente resolveremos, ok?

Partiu?

Passo 2

Vamos então desenhar esse paraboloide e plano que o enunciado nos deu!

Temos um paraboloide

x 2 + y 2 + z = 2

Que quando x , y = 0,0 , z = 2 . E está orientado para baixo, significa que a “cauda” dele está virado para baixo.

Ou seja, temos um paraboloide que seu ponto máximo é em z = 2 .

E também temos um plano

z = 1

Que vai cortar esse paraboloide.

Tudo isso fica assim:

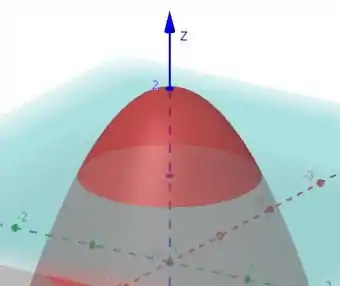
E só queremos essa parte superior como a questão diz!

Tudo certo, vamos para o próximo passo.

Passo 3

Vamos calcular o divergente do campo F → agora:

Temos que

F → x , y , z = z t g - 1 y 2 i → + z 3 ln ⁡ x 2 + 1 j → + z k →

O divergente fica:

∇ ⋅ F → = ∂ ∂ x F x + ∂ ∂ y F y + ∂ ∂ z ( F z )

Sendo F x tudo que acompanha i →

F x = z t g - 1 y 2

F y tudo que acompanha j →

F y = z 3 ln ⁡ x 2 + 1

F z tudo que acompanha k →

F z = z

Vamos ter que

∇ ⋅ F → = ∂ ∂ x z t g - 1 y 2   + ∂ ∂ y z 3 ln ⁡ x 2 + 1 + ∂ ∂ z z

Lembrando que a derivada parcial mantém todas as variáveis como constante, exceto a que estamos derivando em relação.

∂ ∂ x z t g - 1 y 2   = 0

Pois estamos derivando em relação à x

∂ ∂ y z 3 ln ⁡ x 2 + 1 = 0

Pois estamos derivando em relação à y

∂ ∂ z z = 1

Pois estamos derivando em relação à z .   Portanto,

∇ ⋅ F → = 1

Certo? Agora vamos ver a região de integração!

Passo 4

A região de integração é um paraboloide:

Do chão do nosso sólido, que é o plano

z = 1

Até o topo dele, que é o paraboloide

z = 2 - x 2 - y 2

Então, z varia assim:

1 ≤ z ≤ 2 - x 2 - y 2

Em coordenadas cilíndricas temos:

x = r c o s θ y = r s e n θ z = z

Substituindo no paraboloide

z = 2 - r c o s θ 2 - r s e n θ 2

z = 2 - r 2

Então, z vai variar assim em coordenadas cilíndricas:

1 ≤ z ≤ 2 - r 2

Como temos um paraboloide completo, θ percorre todo círculo trigonométrico:

0 ≤ θ ≤ 2 π

Agora, vamos achar o raio r !

Temos que o nosso paraboloide em coordenadas polares é

z = 2 - r 2

Agora, substituindo o plano z = 1 na equação

1 = 2 - r 2

Simplificando

r 2 = 1

r = 1

Show!

Os limites de integração vão ser:

0 ≤ r ≤ 1 0 ≤ θ ≤ 2 π 1 ≤ z ≤ 2 - r 2

E o diferencial de volume em coordenadas cilíndricas vai ser

d V = r d z d r d θ

Agora montando a integral, lembrando que o limite com mais variáveis fica na integral mais de dentro:

∭ E ∇ ⋅ F → d V = ∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2 1 r d z d r d θ

O próximo passo é resolver!

Passo 5

Resolvendo a integral

∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2 1 r d z d r d θ

Primeiro em relação à z :

∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2 1 r d z d r d θ = ∫ 0 2 π ∫ 0 1 2 - r 2 - 1 r d r d θ

Simplificando

∫ 0 2 π ∫ 0 1 2 - r 2 - 1 r d r d θ = ∫ 0 2 π ∫ 0 1 1 - r 2 r d r d θ

Distribuindo o r

∫ 0 2 π ∫ 0 1 1 - r 2 r d r d θ = ∫ 0 2 π ∫ 0 1 r - r 3 d r d θ

Agora em relação à r

∫ 0 2 π ∫ 0 1 r - r 3 d r d θ = ∫ 0 2 π r 2 2 - r 4 4 0 1 d θ

Aplicando os limites

∫ 0 2 π r 2 2 - r 4 4 0 1 d θ = ∫ 0 2 π 1 2 - 1 4 d θ

∫ 0 2 π 1 2 - 1 4 d θ = ∫ 0 2 π - 1 4 d θ

Resolvendo para θ

∫ 0 2 π - 1 4 d θ = - 1 4 . 2 π

- 1 4 . 2 π = - π 2

Logo, nossa resposta é

∭ E ∇ ⋅ F → d V = - π 2

Resposta

∭ E ∇ ⋅ F → d V = - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fluido escoa em movimento uniforme com velocidade v → dada. Verificar se v → representa um possível fluxo incompressível. v → = 2i → + xj → -k →
Dado o campo vetorial vec f , calcular d i v vec f .vec f (x , y , z) = ln x y vec i + x vec j + z vec k
Um fluido escoa em movimento uniforme com velocidade v → dada. Verificar se v → representa um possível fluxo incompressível. v → = 2 x yi → + xj →
Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.d) v → x , y = - y , x
Seja vec u = (x^2 - y^2) * grad f . Calcular div vec u no ponto P ( 1 , 2,3 ) sendo:b) f = x y z + 2 x y