Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 5
Seja a área de um quadrado cujos lados têm comprimento e suponha que varie com o tempo .
(a) Faça uma figura do quadrado com os dados e colocados apropriadamente.
(b) Escreva uma equação que relacione e .
(c) Use a equação de (b) para encontrar uma equação que relacione e .
(d) Em um certo instante, os lados medem e crescem a uma taxa em . Com que rapidez a área está crescendo naquele insante?
Passo 1
(a)
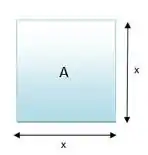
Passo 2
Pela fórmula da área podemos dizer que:
Passo 3
Derivando a equação da letra (b) em relação a teremos:
Passo 4
Bom, nessa ele da dois dados pra gente. O primeiro é que os lados medem , daí tiramos que:
E o segundo dado é que os lados crescem a uma taxa em , ou seja:
Substituindo na expressão encontrada na letra (c), teremos que:
A taxa de variação é de
Resposta
(b)
(c)
(d)