Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 7

Seja V o volume de um cilindro de altura h e raio r , e suponha que h e r variem com o tempo.

(a) Como estão relacionadas d V d t , d h d t e d r d t ?

(b) Em certo instante, a altura é de 6   c m e está crescendo a 1   c m / s , enquanto o raio é de 10   c m e está decrescendo a 1   c m / s . Com que rapidez o volume está variando naquele instante? O volume está crescendo ou decrescendo naquele instante?

Passo 1

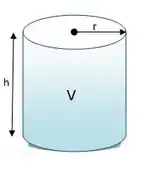
Podemos relacionar essas variáveis escrevendo a fórmula do volume do cilindro:

V = π r 2 h

Passo 2

(a)

Vamos derivar essa expressão em relação a t pra relacionar d V d t , d h d t e d r d t

d V d t   = d π r 2 h d t

d V d t = π d r 2 h d t

Usando a regra da derivada do produto:

d V d t = π   d r 2 d t     h +     r 2 d h d t

Derivando e usando a regra da cadeia, temos que:

d V d t = π   d r 2 d r d r d t     h +     r 2 d h d h d h d t

d V d t = π   2 r h d r d t +     r 2 d h d t

Passo 3

(b)

Nesse enunciado ele dá alguns dados pra gente, vamos ver quais são eles:

Altura de 6   c m e crescendo com 1cm/s, então h = 6 e d h d t = 1

Raio de 10 c m e decrescendo a 1 c m / s ,   então r = 10 e d r   d t = - 1   . Lembrando de atentar pro sinal negativo por estar decrescendo.

Substituindo todos esses dados na expressão que encontramos na letra (b), ficamos com:

d V d t = π   2 r h d r d t +     r 2 d h d t

d V d t = π   2 10   c m 6   c m - 1 c m s +     10   c m 2 1 c m s

d V d t = π   - 120 c m 3 s +     100 c m 3 s

d V d t =   - 20 π c m 3 s

Como d V d t < 0 , o volume está decrescendo naquele instante.

Resposta

(a) d V d t = π   2 r h d r d t +     r 2 d h d t

(b) d V d t =   - 20 π c m 3 s , volume decrescendo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma quadra de softball é um quadrado cujos lados medem 60p é s é de comprimento. Suponha que um jogador correndo da primeira para a segunda base tenha uma velocidade de 25p é s / s é no instante em qu
Um tanque de água cônico com o vértice para baixo tem um raio de 10m no topo e uma altura de 24m . Se a água fluir dentro do tanque a uma taxa de 20m 3 / m i n , com que velocidade sua profundidade es
Um satélite está em uma órbita elíptica em torno da Terra. A sua distância r (em milhas) do centro da Terra é dada por r = 4995 1 + 0,12 cos ⁡ θ Onde θ é o ângulo medido do ponto da órbita mais próxim
Um avião está subindo a um ângulo de 30 ° com a horizontal. Com que rapidez o avião estará ganhando altura se sua velocidade for de 500 milhas por hora?
Para a câmera e o foguete da Figura 3.4.5, a que taxa estará variando a distância entre câmera e foguete quando ele estiver a 4.000p é s é de altura e subindo verticalmente a 880p é s / s é ?