Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 19

Uma quadra de softball é um quadrado cujos lados medem 60   p é s de comprimento. Suponha que um jogador correndo da primeira para a segunda base tenha uma velocidade de 25   p é s / s no instante em que está a 10   p é s da segunda base. Com que taxa estará variando a distância do jogador à base do batedor naquele instante?

Passo 1

Eu sei eu sei, a primeira coisa que você pensou foi “mano o que é softball e aonde são essas primeira e segundas bases?” haha. Por isso vou trazer um desenho pra facilitar a nossa vida. Se liga em como funciona mais ou menos a quadra desse jogo:

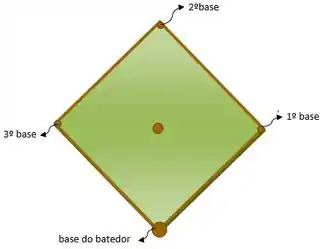
Agora sim né hehe. Então disso a gente já tira que a distância entre a primeira e a segunda bases é basicamente o lado do quadrado, ou seja, 60   p é s .

Então se o jogador está a 10   p é s   da segunda base, ele está a 50   p é s da primeira base concorda? Se tirássemos uma foto do momento estaria assim (e sim o nosso jogador é uma seta vermelha haha):

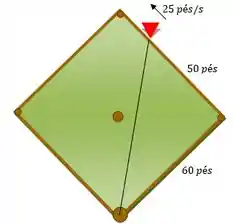
Passo 2

Até aí está tudo lindo, masss como vamos relacionar esses dados com a taxa em que estará variando a distância do jogador à base do batedor? Pra isso vamos precisar de um poquito de geometria

Mas antes vamos chamar a distância do jogador até a primeira base de d 1 , até a segunda base de d 2   e até a base do batedor de d b . Daí já tiramos que:

d d 1 d t = 25   p é s / s

E

d d 2 d t = -   25   p é s / s

Negativo pois d 2 está diminuindo. Além disso estamos interessados em d d b d t .

Agoraaaa sim vamos para a geometria, vê se você concorda com essa figura

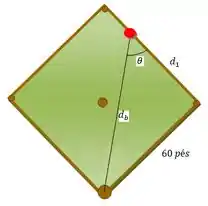
Sim, nosso jogador agora virou uma bolinha vermelha 😊. Aí a gente foi lá e chamou aquele ângulo ali de θ . Mas podemos falar que:

cos ⁡ θ = c a t e t o   a d j a c e n t e h i p o t e n u s a = d 1 d b

  d b   cos ⁡ θ = d 1

Se derivarmos esse cara em relação ao tempo vamos chegar que:

d d t ( d b  cos ⁡ θ ) = d ( d 1 ) d t

Usando a regra da derivada do produto:

d ( d b ) d t cos ⁡ θ + d b d cos ⁡ θ d t = d ( d 1 ) d t

d ( d b ) d t cos ⁡ θ + d b ( - sin ⁡ θ ) d θ d t = d ( d 1 ) d t                               ( e q u a ç ã o   1 )

Passo 3

Além disso podemos também falar que:

sin ⁡ θ = c a t e t o   o p o s t o h i p o t e n u s a = 60 d b

Se derivarmos esse cara em relação ao tempo vamos chegar que:

d d t ( sin ⁡ θ ) = d d t 60 d b

cos ⁡ θ d θ d t = - 60 d b 2 d d b d t                                  

d θ d t = - 60 d b 2 cos ⁡ θ d ( d b ) d t                         ( e q u a ç ã o   2 )

Passo 4

No instante pedido:

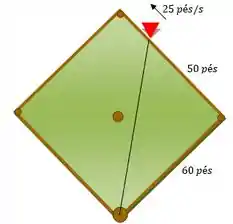
d 1 = 50   p é s , então por Pitágoras temos:

50 2 + 60 2 = d b 2  

d b = 10   61

Então

cos ⁡ θ = d 1 d b = 50 10 61 = 5 61

sin ⁡ θ = 60 d b = 60 10 61 =   = 6 61

Passo 5

Agora podemos relacionar as equações 1 e 2, usando os valores de   cos ⁡ θ e sin ⁡ θ  

d ( d b ) d t cos ⁡ θ + d b ( - sin ⁡ θ ) d θ d t = d ( d 1 ) d t                               ( e q u a ç ã o   1 )

d θ d t = - 60 d b 2 cos ⁡ θ d ( d b ) d t                         ( e q u a ç ã o   2 )

Substituindo (2) em (1):

d ( d b ) d t cos ⁡ θ + d b ( - sin ⁡ θ ) - 60 d b 2 cos ⁡ θ d ( d b ) d t = d ( d 1 ) d t

Substituindo:

d b = 10   61

cos ⁡ θ = 5 61

sin ⁡ θ   = 6 61

d d 1 d t = 25   p é s / s

Ficamos com essa pequeniníssima expressão:

d d b d t 5 61   - 10   61 6 61 - 60 10 61 2 5 61 = 25  

Bom, agora temos duas alternativas: chorar ou fazer as contas haha. Mas se fizer as contas com bastante calma prometo que vai dar certo 😉

d d b d t 5 61   - ( 60 ) - 60 6100 5 61 61 = 25  

d d b d t 5 61   - ( 6 ) - 6 5 61 = 25  

d d b d t 5 61 + 36 5 61 = 25  

d d b d t 25 5 61 + 36 5 61 = 25  

Calmaaa, quase lá

d d b d t 61 5 61 = 25  

d d b d t = 25 5 61 61  

d d b d t =     25 5 61   =     125 61   25   p é s / s

FINALMENTEEEE CHEGAMOS NA NOSSA RESPOSTA

Resposta

  125 61   25   p é s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

35. Dois caminhões aproximam-se de um cruzamento, um deles vindo da direção oeste e outro pelo sul. Se ambos estão com velocidade de kk m / h , mostre que um se aproxima do outro com uma velocidade de
36. Uma tina horizontal tem 16 m de comprimento e seus extremos são trapézios isósceles com uma altura de 4 m, uma base menor de 4 m e uma base maior de 6 m . A água está fluindo entro da tina a uma t
Uma antena de radar está localizada num navio a 16k m de uma praia reta e está girando com 32r p m . Com que velocidade o feixe do radar estará percorrendo a praia quando feixe formar um ângulo de 45
Um avião está voando a uma velocidade constante a uma altitude de 3k m sobre uma linha reta que ira passar diretamente acima de um observador no chão. Num dado instante, o observador nota que o ângulo
5- Se y = x^2 e (d x)/(d t) = 3 , então qual será o valor de (d y)/(d t) quando x = - 1 ?