Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.2 - Ex. 7

Seja

f x = e - 1 x 2     s e     x ≠ 0 0     s e     x = 0

  1. Calcule f ' 0 , pela definição
  2. Determine f '
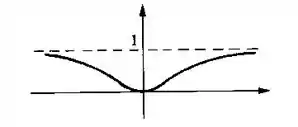
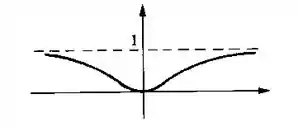
  3. Esboce o gráfico, calculando, para isto, todos os limites necessários

Passo 1

  1. Vamos calcular f ' 0 pela definição. Para quem não lembra a fórmula é essa,

    2. f ' 0 = lim x → 0 ⁡ f x - f 0 x

    Aplicando,

    f ' 0 = lim x → 0 ⁡ e - 1 x 2 - 0 x

    Calculando esse limite, vemos que ele não existe!

    Passo 2

  2. Para calcular f ' x vamos ver as regras que vamos precisar para calcular as derivadas, vamos usar a regra do polinômio e da função exponencial:

    3. x n ' = n x n - 1

    e f x ' = e f x ⋅ f ( x ) '

    Aplicando:

    f ' x = e - 1 x 2 ' = e - 1 x 2 - 1 x 2 ' = e - 1 x 2 - x - 2 '

    Derivando,

    f ' x = e - 1 x 2 - - 2 x - 2 - 1 = e - 1 x 2 2 x - 3

    Ajeitando,

    f ' x = 2 x 3 e - 1 x 2

    Assim:

    f ' x = 2 x 3 e - 1 x 2   s e     x ≠ 0 0     s e     x = 0

    Passo 3

  3. Para esboçar o gráfico vamos calcular os limites de f para x → + ∞ e x → - ∞ :

lim x → + ∞ ⁡ e - 1 x 2 = e 0 = 1

lim x → - ∞ ⁡ e - 1 x 2 = e 0 = 1

Pronto, agora podemos esboçar o gráfico, ficando desse jeito:

Resposta

  1. f ' 0 = 0
  2. f ' x = 2 x 3 e - 1 x 2   s e     x ≠ 0 N ã o   e x i s t e     s e     x = 0
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). f x = - x 4 + 4 x 3 - 4 x 2 + 2
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). f x = x 3 + 2 x 2 + x + 1
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). y = x + 1 x 2
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). f x = 3 x 2 + 4 x 1 + x 2
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). x = t 2 1 + t 2