Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.3 - Ex. 10
Seja definida e derivável no intervalo aberto , com , tal que
a) Mostre que, para todo em , existe e que é contínua em
b) Mostre que existe tal que e em
c) Esboce o gráfico de
Passo 1
a) Como é derivável em , temos contínua nesse intervalo. Assim, vamos tentar derivar usando a regra da cadeia:
Desse modo, para todo em , existe. Além disso, é contínua porque resulta de soma e multiplicação de funções contínuas ( e são contínuas).
Passo 2
b) Como é contínua e , o teorema da conservação do sinal nos diz que existe , com , tal que e pertencem a e para .
Como , sendo a soma de dois quadrados com no intervalo como acabamos de ver, concluímos que .
Além disso, também teremos no mesmo intervalo, pois .
Passo 3
c) Já vimos que, quando , temos , além de . Então, o esboço que temos que fazer deve ser um gráfico crescente e com concavidade para cima, tipo assim:
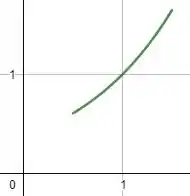
Beleza?
Resposta
Ei, a resposta está no passo a passo :)