Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.4 - Ex. 4
- Seja
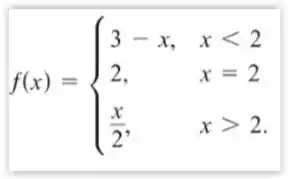
- Determine e e .
- Existe ? Em caso afirmativo, qual é? Em caso negativo por que não?
- Determine e .
- Existe ? Em caso afirmativo, qual é? Em caso negativo, por que não?
Passo 1
Letra a e b)
Vindo pela direita função encontra um ponto aberto em uma casas para cima de y, o que seria 1 , além de estar na reta :
Vindo pela esquerda a função encontra um ponto aberto em uma casa para cima de y, o que seria 1, além de estar na reta :
Por possuírem valores iguais então temos bilateralidade. Logo o limite em 2 é igual a 1.
Passo 2
Em a função é um ponto contínuo da reta , logo ela é a mesma vindo pela esquerda e pela direita e por isso possui limite bilateral no mesmo ponto.
Logo:
Resposta
a),
b) , tem bilateralidade pois a esquerda e a direita temos o mesmo limite.
c)
d) Existe e vale , pois temos a bilateralidade vinda dos limites a esquerda e a direita de 4.
Exercícios de Livros Relacionados
40- Prove as afirmações de limite nos Exercícios 37-50 lim x → 0 4 - x = 2
Cada um dos Exercícios 31-36 dá uma função f ( x ) , um ponto x 0 e um número positivo ϵ . Determine L = lim x → x 0 f ( x ) . Em seguida, determine um número δ0 de modo que para todo x . 0x - x 0δ
45- Prove as afirmações de limite nos Exercícios 37-50 lim x → - 3 x 2 - 9 x + 3 = - 6
Cada um dos Exercícios 31-36 dá uma função f ( x ) , um ponto x 0 e um número positivo ϵ . Determine L = lim x → x 0 f ( x ) . Em seguida, determine um número δ0 de modo que para todo x . 0x - x 0δ
50- Prove as afirmações de limite nos Exercícios 37-50 lim x → 0 x 2 sin 1 x = 0