Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.1 - Ex. 20

Seja f t = 1 / t para t ≠ 0 .

  1. Determine a taxa de variação média de f com relação a t nos intervalos (i) de t = 2 a t = 3 e (ii) de t = 2 a t = T .
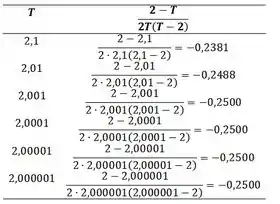
  2. Faça uma tabela de valores da taxa média de variação de f com relação a t no intervalo 2 ,   T , para alguns valores de T que se aproximem de 2 , como T = 2,1 ,   2,01 ,   2,001 ,   2,0001 ,   2,00001 e 2,000001 .
  3. O que a sua tabela indica é a taxa de variação de f com relação a t em t = 2 ?
  4. Calcule o limite, quando T se aproxima de 2 , da taxa de variação média de f com relação a t no intervalo de 2 a T . Você precisará fazer alguns cálculos algébricos antes de substituir T = 2 .

Passo 1

Lembrando que o coeficiente angular é calculado por:

a = ∆ f ∆ t

Assim,

a 1 = ∆ f ∆ t = f 3 - f 2 3 - 2 = 1 3 - 1 2 3 - 2 = - 1 6

a 2 = ∆ f ∆ t = f T - f 2 T - 2 = 1 T - 1 2 T - 2 = 2 - T 2 T T - 2 = 2 - T 2 T T - 2

Passo 2

Agora vamos fazer uma tabela de valores para taxa média de variação de g .

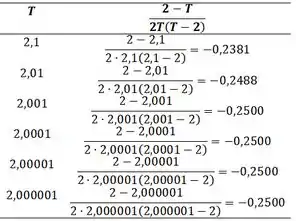
Passo 3

Como podemos ver pela letra b.), o coeficiente angular tende a - 0,25 quando vamos diminuindo o valor de T para valores próximos a 2 , portanto

a 2 = - 0,25

Passo 4

Vamos agora calcular o limite de ∆ f / ∆ t :

lim T → 2 ⁡ 2 - T 2 T T - 2

Como podemos ver, substituindo T = 2 dá ruim:

lim T → 2 ⁡ 2 - T 2 T T - 2 = 2 - 2 2 ∙ 2 2 - 2 = 0 0

Portanto, precisamos fazer algumas mexidas na equação:

lim T → 2 ⁡ 2 - T 2 T T - 2 = lim T → 2 ⁡ 2 - T - 2 T 2 - T = lim T → 2 ⁡ 1 - 2 T = 1 - 2 ∙ 2 = - 1 4 = - 0,25

Resposta

  1. a 1 = - 1 6 ;   a 2 = 2 - T 2 T T - 2

  3. - 0,25
  4. - 0,25
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 61-66, você aprofundará a exploração determinando deltas grafica1nente. Utilize um SAC para executar as seguintes etapas:Trace a função y=f ( x ) próximo ao ponto x 0 sendo aproximado.D
Nos Exercícios 61-66, você aprofundará a exploração determinando deltas grafica1nente. Utilize um SAC para executar as seguintes etapas:Trace a função y=f ( x ) próximo ao ponto x 0 sendo aproximado.D
Nos Exercícios 61-66, você aprofundará a exploração determinando deltas graficamente. Utilize um SAC para executar as seguintes etapas:Trace a função y=f ( x ) próximo ao ponto x 0 sendo aproximado.De
Nos Exercícios 61-66, você aprofundará a exploração determinando deltas grafica1nente. Utilize um SAC para executar as seguintes etapas:Trace a função y=f ( x ) próximo ao ponto x 0 sendo aproximado.D
Faça o gráfico da função f x = e x + ln ⁡ | x - 4 | para 0 ≤ x ≤ 5 . Você acha que o gráfico é uma representação precisa de f ?Como você faria para que o gráfico represente melhor f ?