Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.3 - Ex. 46
Seja
- Encontre e .
- Existe ?
- Esboce o gráfico de .
Passo 1
Olá, meu querido estudante. Pronto para mais uma resolução?
Então, vamos aqui responder 3 pequenas questões sobre a função dada.
Iremos encontrar os limites laterais da função dada quando nos aproximamos de . Iremos responder se o limite de e por último iremos esboçar o gráfico da função.
Para encontrarmos o limite lateral da função deveremos prestar atenção em qual das duas equações deveremos utilizar quando formos ao encontro de pela direita ou pela esquerda.
Para que exista, os limites laterais que iremos calcular na letra a) devem ser iguais, caso sejam diferentes o limite de para não existe.
O gráfico da função iremos fazer juntos utilizando o GeoGebra, mas irei te explicar como você pode fazer na mão e em quais pontos você deve prestar atenção.
Passo 2
- Para calcularmos o limite lateral deveremos prestar atenção em quais equações representam a função quando formos pelo lado direito, para valores infinitesimalmente maiores que .
- Veja que os limites laterais da função no ponto de limite analisado são diferentes, sendo assim o limite
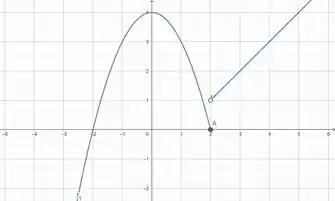
- Vamos agora para a construção do gráfico. Para construir esse gráfico, devemos nos atentar ao ponto de inflexão, o ponto onde as equações que regem nossa função se juntam. Veja que é um ponto onde pode ser igual a . Sendo assim, na representação gráfica este local deve possuir um círculo fechado, indicando isso, diferente de que deve possuir um círculo aberto.
Nesses casos, temos que
Para calcularmos o limite lateral deveremos prestar atenção em quais equações representam a função quando formos pelo lado direito, para valores infinitesimalmente menores que .
Nesses casos, temos que
Passo 3
Não existe.
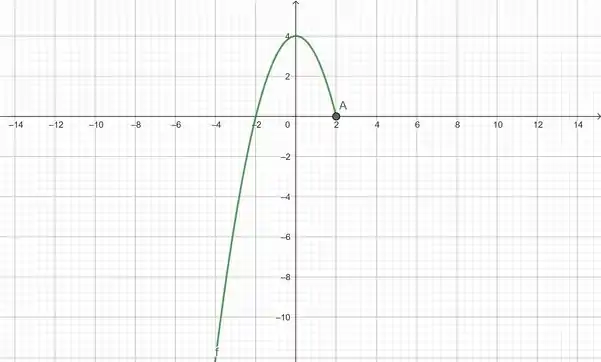
Primeiro vamos então inserir no gráfico, isso para valores . Temos aqui uma parábola, com o termo , sendo assim o eixo corta o vértice da parábola. Por possuir o coeficiente sua parábola é virada para baixo.
Agora vamos inserir Temos aqui uma reta, por termos ela é crescente e corta o eixo em .
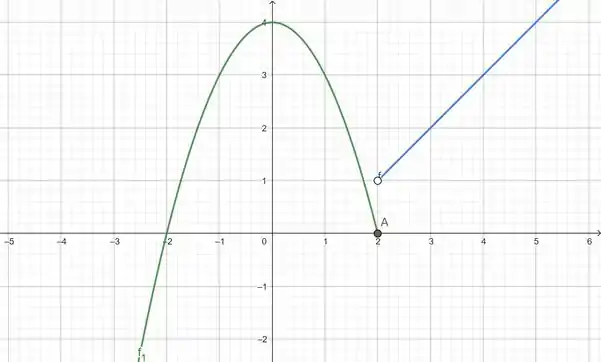
Resposta
- Não existe
