Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 88
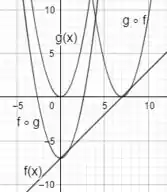
Seja e . Faça o gráfico de e juntamente com e .
Passo 1
Então galera, antes de começarmos a resolver esse exercício vamos dar uma relembrada no na principal característica de uma função composta, tudo bem?
Quando dizemos que a função é composta de , como aparece em um dos casos que temos, estamos dizendo que a imagem de vira o domínio de . Descrevendo matematicamente isso, teremos o seguinte:
Para o contrário isso também é válido, isto é, quando dizemos que a função é composta de , estamos dizendo que a imagem de vira o domínio de . Dessa forma, teremos:
Tendo isso fixado na mente, vamos para a resolução!
Passo 2
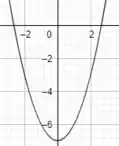
Fazendo primeiro , temos que:
Cujo gráfico é:
Passo 3
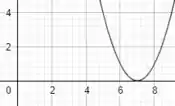
Agora fazendo , temos que:
Cujo gráfico é:
Passo 4
Por fim, unindo os 4 gráficos em apenas um plano, temos:
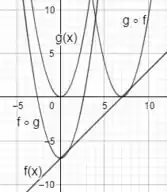
Resposta
Exercícios de Livros Relacionados
Suponha que f seja uma função par, g seja uma função ímpar e tanto f como g sejam definidas na reta real ℝ. Quais das seguintes funções (quando definidas) são pares? E ímpares? b )f g
Suponha que f seja uma função par, g seja uma função ímpar e tanto f como g sejam definidas na reta real ℝ. Quais das seguintes funções (quando definidas) são pares? E ímpares? c )g f
Suponha que f seja uma função par, g seja uma função ímpar e tanto f como g sejam definidas na reta real ℝ. Quais das seguintes funções (quando definidas) são pares? E ímpares? f )f ∘ g
Faça o gráfico da função: y = 2 x ² + 1 ² Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.
O exercício a seguir apresenta uma equação de elipse. Coloque a equação no formato padrão e esboce a elipse. 9 x 2 + 25 y 2 = 225