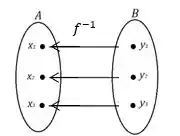
- Seja uma função injetora com domínio e imagem . Como é definida a função inversa ? Qual o domínio de ? Qual a imagem de ?
Passo 1
Olá, meu amigo. Yuri aqui pronto para te ajudar a resolver mais uma atividade.
Essa atividade é teórica, então devemos pensar um pouco mais na situação.
Bom, a função inversa é definida como aquela que associa cada valor da imagem de a um valor do domínio da , literalmente o inverso.
Já uma função injetora, também conhecida como função injetiva, é um tipo de função matemática entre dois conjuntos, onde elementos distintos do conjunto de origem são mapeados em elementos distintos no conjunto de destino.
Passo 2
A função inversa é uma operação matemática que "desfaz" o efeito de outra função. Dada uma função , a função inversa, denotada por , é aquela que retorna o valor original de quando aplicada a . Em outras palavras, se , então .
Nem toda função tem uma função inversa. Para que uma função tenha uma inversa, ela deve ser injetora, o que significa que cada valor de está associado a um único valor de . Além disso, a função deve ser sobrejetora, o que significa que existe pelo menos um valor de para cada valor possível de .
A notação é usada para representar a função inversa, e não indica uma potência negativa. A função inversa é, essencialmente, uma reversão da função original.
Por exemplo, se tivermos uma função , a função inversa desfaz essa operação, e pode ser expressa como . Quando você aplica ao resultado de , obtém de volta o valor original de .
Passo 3
Exemplo:
é o domínio e é a imagem de
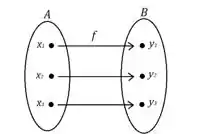
A função vai ser:
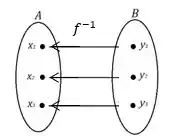
Passo 4
Como podemos ver na figura do passo 2, �� o domínio de e é o contradomínio. Exatamente o inverso do que era em !
Resposta