Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 55
A queda de uma pedra em uma lago gera ondas circulares que se espalham a uma velocidade de .
(a) Expresse o raio desse círculo como uma função do tempo (em segundos).
(b) Se é a área do círculo como uma função do raio, encontre e interprete-a.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
Bom, o exercício nos diz que a queda da pedra gerou ondas circulares que se espalham a cada segundo.
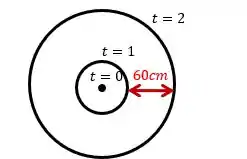
Esse é o valor que o raio aumenta a cada segundo, porque o quanto a onda se espalhou (seta vermelha na figura) é medido através da diferença entre um círculo e outro dentro de um período de tempo, assim como na figura:
Na letra (a) queremos saber a função que descreve o valor do raio de acordo com o tempo e em (b) queremos entender a função composta da área do círculo e do crescimento do raio.
Ah, vale lembrar que uma função composta do tipo é dada da seguinte forma:
Agora vamos por partes! 😉
Passo 2
Vamos criar uma função que nos dê o valor do raio de acordo com o tempo que se passou da queda.
Como ele aumenta a cada segundo, podemos pegar a varíavel e multiplicar pelo tanto que o raio cresce a cada segundo:
Beleza, temos a nossa função.
Aqui, o raio depende do tempo , por isso a notação .
Passo 3
Agora, para a letra (b), temos que lembrar da área do círculo:
E então fazer a função composta , substituindo todo da função pela função inteira de .
Calculando, temos:
Okay, mas o que isso significa?
Essa função agora indica a área do círculo que a onda formou, tem como base apenas o tempo.
Quando substituímos todo de pela função achada na letra (a), estamos indicando que o raio segue certa “regra”, então conseguimos saber a área tendo somente o tempo desde a queda , sem precisar fazer o cálculo do raio.
Valeu, galera! Até a próxima! 😉
Resposta
(a)
(b) , que é a área do círculo em função do raio apenas.