Seja o hemisfério e suponha que seja uma função contínua com

Dividindo em quatro retalhos, estime o valor de .

E ai galera, beleza!?

Nessa questão devemos estimar o valor da integral abaixo dividindo H em quatro retralhos.

Onde, é o hemisfério:

Sabemos também que:

Antes de tudo, vamos lembrar como escrevemos a soma de Riemann:

Sabendo disso, galera, nós podemos usar os planos e para dividir em quatro pedaços de tamanhos iguais, cujas áreas de superfície serão iguais a da área de superfície de uma esfera de raio . Desse jeito:

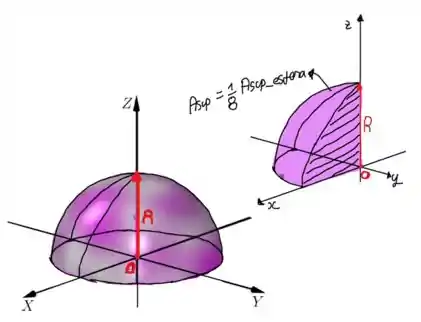
Sabendo que a área da superfície de uma esfera é:

Assim, vamos ter nossa área igual a:

Agora não tem erro pessoal, é so aplicarmos na soma de Riemann.

Bora fazer isso!