Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 59
(a) Mostre que as equações paramétricas , representam um elipsoide.
(b) Use as equações paramétricas da parte (a) para traçar o gráfico do elipsoide para o caso .
(c) Determine, mas não calcule, a integral dupla que dá a área de superfície da parte do elipsoide da parte (b).
Passo 1
E aí, meus pipowssss... Tudo belezinha? 😊
Precisamos, no item (a), mostrar que as equações paramétricas abaixo representam um elipsoide:
Já no item (b), iremos representar graficamente a elipsoide do item (a) quando
E no item (c), sem calcular, descobrir a fórmula da área de superfície da parte do elipsoide do gráfico em (b).
Show de bola! =D
Passo 2
(a) Galera, a fórmula para a superfície do elipsoide é dado por
Se a gente fizer
Ou seja, as equações paramétricas satisfazem a equação do elipsoide!
Passo 3
(b) Agora vamos traçar o gráfico do elipsoide. Substituindo
Na fórmula do elipsóide, teremos:
Colocando isso num software top, teremos:
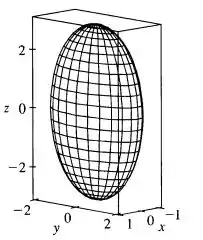
Passo 4
(c) Pessoal, para descobrir a integral dupla para a área de superfície, temos essa fórmula aqui:
Utilizando nas equações paramétricas, podemos calcular nosso :
Com o que temos do item (a), teremos:
Substituindo em , podemos fazer as derivadas parciais de em relação a e a :
Então, temos agora nosso produto vetorial dado por
Resolvendo por qualquer método, chegaremos a
Calculando agora o módulo desse produto vetorial, que é a soma de todos os termos ao quadrado dentro de uma raiz, teremos
Show! Podemos assim escrever a integral dupla que dá a área da superfície, com os limites de integração dados no enunciado:
Assim,