Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 49

49. Seja

g (x) = (x^2 + x - 6)/(|x - 2|)

  1. ( i ) . underset(x -> 2^+)(lim) g ( x ) ( i i ) . underset(x -> 2^-)(lim) g ( x )

  2. underset(x -> 2)(lim) g ( x ) existe?
  3. Esboce o gráfico de g .

Passo 1

Olá, meu nobre amigo, Yuri aqui e estarei te ajudando a resolver essa atividade de limites.

A atividade nos pede para resolvermos alguns limites, sendo que g (x) possui um modulo no seu denominador. Isso faz com que precisemos analisar o sinal da função do denominador pois a depender do intervalo em que formos calcular o limite, teremos a função do denominador ou seu oposto.

E pra relembrar os limites laterais:

  • em underset(x -> 2^+)(lim) g ( x ) estamos nos aproximando de 2 pela direita, ou seja, por valores maiores que 2
  • em underset(x -> 2^-)(lim) g ( x ) estamos nos aproximando de 2 pela esquerda, ou seja, por valores menores que 2

Passo 2

Para o item (a), temos o seguinte:

underset(x -> 2^+)(lim) g ( x )

Como estamos vindo da direita, estamos no caso em que x > 2 . Então o x - 2 sai do modulo com sinal positivo. Pois no estudo dos sinais de |x - 2| = (x - 2) s e (x - 2 > 0) .

Assim,

underset(x -> 2^+)(lim) g ( x ) = underset(x -> 2^+)(l i m) (x^2 + x - 6)/(( x - 2 ))

Para x = 2 :

underset(x -> 2^+)(l i m) (x^2 + x - 6)/((x - 2)) = (4 + 2 - 6)/(0) = (0)/(0)

Opaa, deu uma indeterminação. Então vamos ter que arrumar as coisas pra tirar essa indeterminação!

g (x) = (x^2 + x - 6)/(( x - 2 ))

Olhando para o numerador:

x^2 + x - 6 = ( x - 2 ) ( x + 3 )

Logo,

underset(x -> 2^+)(l i m) (x^2 + x - 6)/((x - 2)) = (( x - 2 ) ( x + 3 ))/(x - 2)

Simplificando, temos:

underset(x -> 2^+)(l i m) (x^2 + x - 6)/((x - 2)) = x + 3

Para x = 2 :

underset(x -> 2^+)(l i m) (x^2 + x - 6)/((x - 2)) = 2 + 3 = 5

Passo 3

Agora vamos olhar o caso underset(x -> 2^-)(lim) g ( x ) . Como estamos vindo pela esquerda, isto é, x < 2 então o termo x - 2 sai do modulo com sinal negativo. Pois |x - 2| = (- x + 2) s e (x - 2 < 0)

Logo,

g (x) = (x^2 + x - 6)/(- ( x - 2 ))

Agora vamos usar a fatoração lá do Passo 2 para não cairmos novamente na indeterminação. Assim,

g (x) = ((x - 2) * (x + 3))/(- ( x - 2 ))

Simplificando:

g (x) = - ( x + 3 )

Portanto,

underset(x -> 2^-)(lim) g (x) = underset(x -> 2^-)(lim) - (x + 3)

Para x = 2 :

underset(x -> 2^-)(lim) g (x) = - 5

Passo 4

(b) Para existir underset(x -> 2)(lim) g ( x ) , os limites laterais precisam ser iguais. Como os limites laterais são diferentes, underset(x -> 2)(lim) g ( x ) não existe!

underset(x -> 2^+)(lim) g (x) = 5

underset(x -> 2^-)(lim) g (x) = - 5

Passo 5

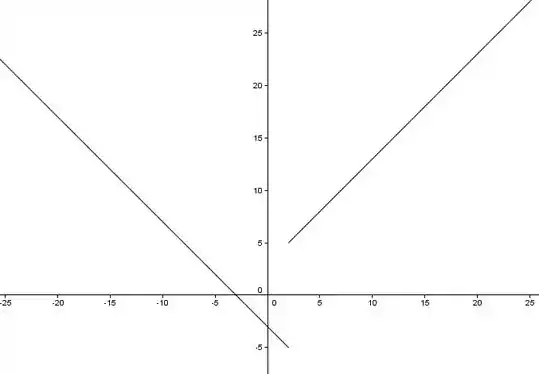
(c) Agora é só esboçarmos o gráfico, vamos utilizar o GeoGebra para isso:

x < 2 :

g (x) = ( x + 3 )

x > 2 :

g (x) = - ( x + 3 )

Logo,

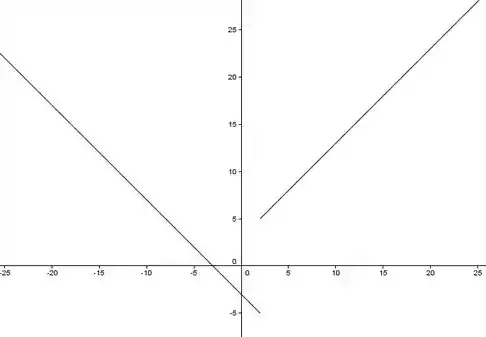
Resposta

  1. underset(x -> 2^+)(lim) g (x) = 5

    underset(x -> 2^-)(lim) g (x) = - 5

  2. Não existe.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os limites quando x → ∞ e quando x → - ∞ . Use essa informação, bem como os interceptos, para fazer um esboço do gráfico, como no Exemplo 11. y = 2 + x 3 1 - x 3 - x
Encontre os limites quando x → ∞ e quando x → - ∞ . Use essa informação, bem como os interceptos, para fazer um esboço do gráfico, como no Exemplo 11. y = x + 4 5 x - 3 4
Faça um esboço da curva y = x n ( n um inteiro) para os cinco casos abaixo:i) n = 0 ii) n0 ,ní m p a r í iii) n0 ,np a r iv) n0 ,ní m p a r í v) n0 ,np a r Então use este esboço para encontrar os segu
Faça um esboço da curva y = x n ( n um inteiro) para os cinco casos abaixo:i) n = 0 ii) n0 ,ní m p a r í iii) n0 ,np a r iv) n0 ,ní m p a r í v) n0 ,np a r Então use este esboço para encontrar os segu
Faça um esboço da curva y = x n ( n um inteiro) para os cinco casos abaixo:i) n = 0 ii) n0 ,ní m p a r í iii) n0 ,np a r iv) n0 ,n �� í m p a r ��í v) n0 ,np a r Então use este esboço para encontrar o