Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.6 - Ex. 47
Encontre os limites quando e quando . Use essa informação, bem como os interceptos, para fazer um esboço do gráfico, como no Exemplo 11.
Passo 1
Fala galera, tudo bem? Bora resolver essa questão! Temos essa função aqui
E precisamos achar os limites dessa função quando
E também
E pede também para esboçarmos o gráfico! Ué, mas como assim?
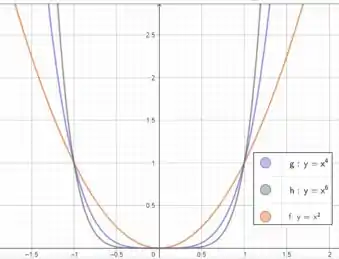
Bom, note que nossa função é um polinômio, e pela maior potência podemos ter um esboço dessa função! Se a maior potência for uma potência par, as duas pontas da função apontam para o mesmo lado
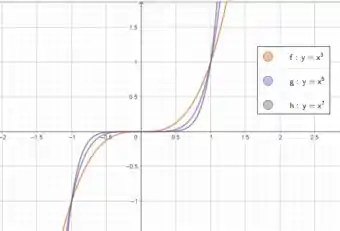
Mas se a maior potência for ímpar vamos ter uma ponta apontando para cima e a outra para baixo, assim
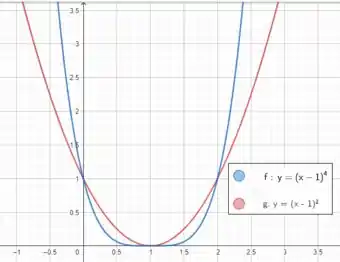
Já se temos raízes, a cara do polinômio vai ficar a mesma, mas passando nas raízes antes do comportamento final no infinito! Veja o exemplo de e . Aqui temos que é raiz de multiplicidade dois e quatro respectivamente
Então a ideia é usar essas estratégias para ver como é nossa função!
Mas relaxa, vou fazer com você!!
Passo 2
Nesse passo vamos tentar caracterizar os pontos principais: onde a função corta o eixo e o eixo .
Primeiramente faremos os interceptos que são os pontos, que são os pontos que tocam o eixo e eixo .
Lembrando que caso o ponto seja raiz duas vezes (par de vezes). O gráfico naquele ponto não corta o eixo . Ele apenas toca em no eixo . Como uma parábola de raiz única!
Nossa função
Para o eixo , é só jogar
Para o eixo é só fazermos
As raízes serão:
Lembrando que o é raiz de multiplicidade par, então não haverá corte em , apenas toca nesse ponto.
Passo 3
Bora verificar os limites?
Agora faremos os limites e depois :
Anotaremos os limites individualmente:
Então:
E agora para o lado negativo:
Anotaremos os limites individualmente:
Então:
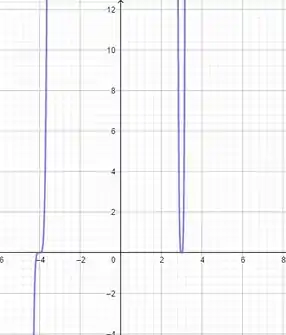
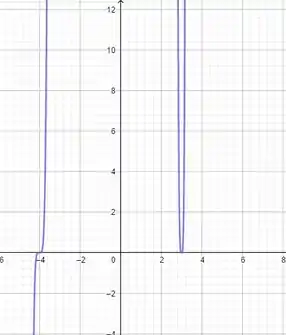
Tudo conforme imaginamos, para valores muito grandes e negativo, a função também é negativa. Os interceptos em são e em o gráfico não muda de sinal apenas toca em . E para valor muito grande positivo, a função é negativa.
Resposta
