Encontre os limites quando e quando . Use essa informação, bem como os interceptos, para fazer um esboço do gráfico, como no Exemplo 11.

Vamos começar com:

Podemos escrever:

No primeiro limite temos:

Então:

Agora, calculando os limites individualmente:

Então:

Agora vamos calcular:

Olhando pra cada limite individualmente:

Então:

Show, bora começar a pensar no esboço do gráfico?!

Teremos um produto de parcelas, então quando qualquer uma dessas parcelas for igual a zero. Assim temos:

Agora vamos calcular quando a curva toca o eixo . Isso acontece quando :

Então temos os pontos .

Agora a gente vai pensar nas informações que a gente tem! Trazendo a função pra pertinho da gente também:

• Pra valores de muito grandes e negativos o vai pra menos infinito;
• Em a curva intercepta o eixo . Se antes disso o tava vindo do infinito negativo e o do infinito negativo, então essa curva toca o eixo de baixo pra cima e da esquerda pra direita;
• Em a curva intercepta o eixo em ;
• Em a curva intercepta o eixo ;
• Se a gente dar uma olhada na nossa curva percebemos que para o é sempre positivo. Isso significa que a curva sai do e cruza o eixo , não apenas toca!
• Em a curva toca no eixo . Como depois disso, em temos então podemos deduzir que no intervalo o cresce, chega a um máximo e depois decresce tocando no eixo em .
• Para temos um . Então podemos inferir que em o descrece, chega a um mínimo e depois volta a crescer, tocando o eixo em .
• A medida que cresce, vai pra infinito!
• Quando calculamos os limites a gente viu que o tendia pra infinito mas o era a multiplicação de infinitos. Isso significa que o sempre vai pra infinito mais rápido que o .

Finalmente podemos plotar a nossa curva:

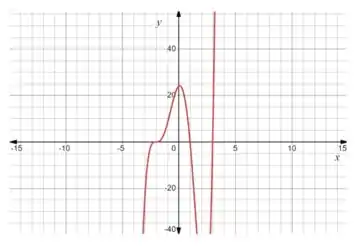
Prontinho!!!