Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 96
Seja Mostre que a equação tem uma solução no intervalo [3,4] e use o métdo de Newton para determiná-la.
Passo 1
Pelo teorema do valor intermediário, temos:
Provamos que existe raiz no intervalo dado.
Passo 2
Aplicando o método de Newton para
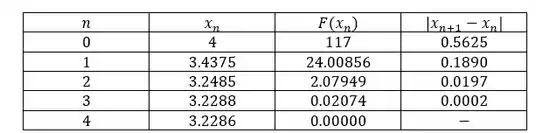
A solução será:
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 4, use o método de Newton para encontrar a raiz real da equação dada com quatro casas decimais. x 3 - 4 x 2 + 2 = 0
Nos exercícios de 1 a 4, use o método de Newton para encontrar a raiz real da equação dada com quatro casas decimais. x 5 - x + 1 = 0
Nos exercícios de 5 até 10, use o método de Newton para encontrar o valor aproximado da raiz indicada com erro menor que um milésimo. x 3 - 2 x + 7 = 0 ; a raiz negativa
Seja a equação f ( x ) = x - x l n ( x ) = 0 . Construa tabelas como as dos exemplos do final do capítulo para a raiz positiva dessa equação. Use ϵ = 1 0 - 5 . Compare os diversos métodos considerando
Baseado no algoritmo de Newton, escreva um algoritmo para este método;Aplique na resolução da equação x 3 - 9 x + 3 = 0 , x 0 = - 1,275 , λ = 0,05 e ε = 0,05 .