Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 90

A figura a seguir apresenta dois cones circulares retos, um de cabeça para baixo dentro do outro. As duas bases são paralelas, e o vértice do menor coincide com o centro da base maior. Que valores de r e h darão ao cone o menor e o maior volume possível ?

Passo 1

Relacionando os valores r   e h   com os valores da altura e do raio do cone maior R e H ,   respectivamente.

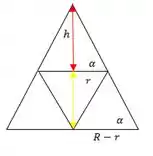
Triângulo Vermelho :

t g α = H - h r

Triângulo amarelo:

t g α = h R - r

Passo 2

Igualando as tangentes:

H - r r = h R - r

h = H R - r R

Passo 3

O volume do cone interno é dado por:

V o l = π r ² h 3

Passo 4

Substituindo a equação do passo 2 na equação do volume:

V o l = π r ² h 3 = π r ² H ( R - r ) 3 R

Passo 5

Encontrando os pontos críticos da equação do volume:

d V o l d r = d π r 2 H R - r 3 R d r = π 2 r H R - r 3 R + π r 2 H - 1 3 R

d V o l d r = π H 3 R 2 r R - 2 r 2 - r 2

d V o l d r = π H 3 R 2 r R - 3 r 2

d V o l d r = 0  

π H 3 R 2 r R - 3 r 2 = 0  

Os pontos são:

r = 0

r = 2 R 3

Passo 6

Quando r = 0 implica em volume V o l = 0

Quando r = 2 R 3 implica em volume V o l = 4 π H R 2 81

Assim, concluímos que o volume mínimo é: V o l = 0 , e o volume máximo: V o l = 4 π H R 2 81

Resposta

Mínimo: V o l = 0   polegadas cúbicas

Máximo: V o l = 4 π H R 2 81 = 67   polegadas cúbicas

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o ponto sobre a reta y = 4 x + 7 que está mais próximo da origem.
Encontre, com precisão de duas casas decimais, as coordenadas do ponto na curva y = t a n ⁡ ( x ) que está mais próximo do ponto ( 1,1 )
Mostre que de todos os retângulos com um área dada, aquele com menor perímetro é um quadradoMostre que de todos os retângulos com um perímetro dado, aquele com menor área é um quadrado
Encontre o ponto sobre a reta 6 x + y = 9 que está mais próximo do ponto ( - 3,1 )
Encontre os pontos sobre a elipse 4 x 2 + y 2 = 4 que estão mais distantes do ponto ( 1,0 )