Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 20
Seja a equação
Construa tabelas como as dos exemplos do final do capítulo para a raiz positiva dessa equação. Use
Compare os diversos métodos considerando a garantia e rapidez de convergência e eficiência computacional em cada caso.
Passo 1
Fala aí pessoal, vamos começar essa questão daqui achando essa raíz por cada método possível!
Vamos dar uma olhada na
Sabemos que ,
então:
Agora a gente já sabe que nossa raiz tá entre e
Passo 2
Vamos começar fazendo o método da bissecção, escolhendo o intervalo como
Aplicando o método da bissecção, a gente chega em:
Passo 3
Vamos agora, usar o método da posição falsa, com o intervalo
Aplicando o método, chegamos em:
Passo 4
Vamos agora, usar o método do ponto fixo, sabemos que :
Precisamos achar uma função , tal que:
Então:
Aplicando o método, com nossa e chegamos em:
Passo 5
Vamos agora, usar o método de Newton.
Primeiro temos nossa .
Agora precisamos calcular a derivada,
Aplicando o método na fórmula, chegamos em:
Passo 6
Vamos começar fazendo o método da secante, escolhendo e
Aplicando o método da secante, a gente chega em:
Passo 7
Agora é só montar a tabela!
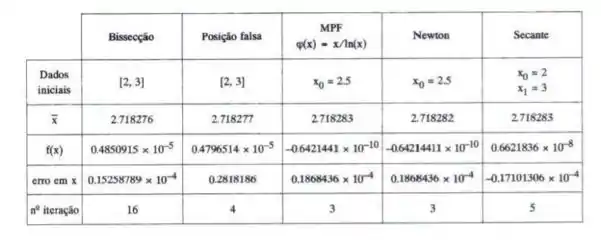
Resposta
