Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 73

Seja

g x = ∫ 0 x f t d t

Onde f é a função cujo gráfico está mostrado.

  1. Em que valores de x ocorrem os valores de máximos e mínimos locais em g ?
  2. Onde g atinge seu valor máximo absoluto?
  3. Em que intervalos g é côncavo para baixo?
  4. Esboce o gráfico de g .

Passo 1

Galera nessa questão temos uma função g ( x ) que é dada por:

g x = ∫ 0 x f t d t

Temos que pelo Teorema Fundamental do Cálculo:

g ' x = f x

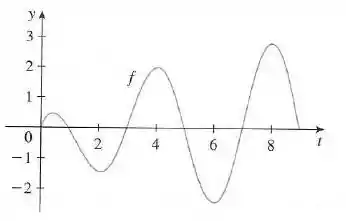
E como a função f é dada pelo seguinte gráfico:

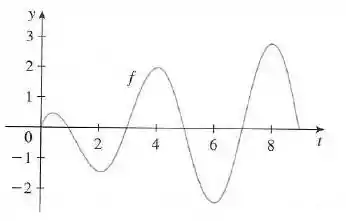
Na realidade o que temos aqui é o gráfico da derivada de g ( x ) .

A partir disso, devemos responder quais são os pontos máximos e mínimos locais de g ( x ) . Onde g atinge seu máximo absoluto, em que intervalos g é concâva para baixo e por fim esboçar um gráfico para a função g ( x ) .

Passo 2

Temos um ponto de máximo ou mínimo quando g ' x = 0 .

Se a derivada está indo de um valor positivo para um negativo, esse é um ponto de máximo e se estiver indo de um valor negativo para um positivo, esse é um ponto de mínimo.

Analisando o gráfico, podemos ver que

  1. Os pontos de máximo são : x = 1   e   x = 5
  2. Os pontos de mínimo são : x = 3   e   x = 7

Note que o ponto x = 9 não é um ponto de máximo e nem de mínimo local pois a função não está definida para x > 9

Passo 3

Podemos dizer que:

g x - g 0 = ∫ 0 x g ' ( x ) d x

E como a derivada de g ( x ) é a função f ( x ) , temos então que:

g x - g 0 = ∫ 0 x f ( x ) d x

Pelo gráfico vemos que

∫ 0 1 f t d t < ∫ 1 3 f t d t < ∫ 3 5 f t d t < ∫ 5 7 f t d t < ∫ 7 9 f t d t

Sabemos que

g 1 = ∫ 0 1 f t d t + g ( 0 )

g 5 = ∫ 0 5 f t d t = g 1 - ∫ 1 3 f t d t + ∫ 3 5 f t d t + g ( 0 )

E

g 9 = ∫ 0 9 f t d t = g 5 - ∫ 5 7 f t d t + �� 7 9 f t d t

Então, temos que g 1 < g 5 < g ( 9 ) .

Então o máximo absoluto ocorre em x = 9 , pois é nesse ponto onde a função g ( x ) está em seu máximo.

Uma forma de avaliar isso intuitivamente é a partir da área abaixo da derivada. A área abaixo da derivada te dá o valor da variação da função g ( x ) .

Á r e a = Δ g ( x )

O ponto aonde você obtêm a maior área nesse gráfico é o ponto x = 9 e por isso esse é o ponto onde a função g ( x ) é o maior possível.

Passo 4

Temos que g é côncava para baixo quando g ' ' x < 0 .

A segunda derivada g ' ' é negativa quando a primeira derivada g ' é decrescente.

Olhando para o gráfico, vemos que f ( x ) é decrescente nos seguintes intervalos:

1 2 , 2 ,   4,6   e   8,9

Passo 5

Esboçando o gráfico sabemos que teremos pontos de máximo em x = 1 ,   x = 5 e pontos de mínimo em x = 3 ,   x = 7 .

Teremos um máximo absoluto em x = 9 e nesse ponto a inclinação da função deve se aproximar de zero.

Teremos concavidade para baixo nos intervalos:

1 2 , 2 ,   4,6   e   8,9

E concavidade para cima nos intervalos:

0 , 1 2 ,   2,4   e   ( 6,8 )

De forma que podemos fazer o seguinte gráfico:

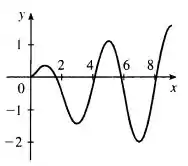
Repare que o máximo absoluto, como vimos no Passo 3 ocorre em x = 9 .

Resposta

  1. Os pontos de máximo são : x = 1   e   x = 5

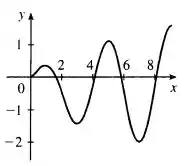
    2. Os pontos de mínimo são : x = 3   e   x = 7

  2. x = 9
  3. 1 / 2,2 ,   4,6   e   8,9
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para cada uma das seguintes funções, faça o gráfico f ( x ) sobre [ a , b ] e f ( x + c ) sobre [ a - c , b - c ] para se convencer de que a Equação I é razoável. f x = x - 4 , a = 4 ,b = 8 e c = 5
Demonstre que se f for ímpar, int_(- a)^a f (x) d x = 0
Para cada uma das seguintes funções, faça o gráfico f ( x ) sobre [ a , b ] e f ( x + c ) sobre [ a - c , b - c ] para se convencer de que a Equação I é razoável. f x = s e n x , a = 0 ,b = π e c = π
Usando substituição, prove que ,para quaisquer números positivosx e y ∫ x x y 1 t d t =∫ 1 y 1 t d t
Para cada uma das seguintes funções, faça o gráfico f ( x ) sobre [ a , b ] e f ( x + c ) sobre [ a - c , b - c ] para se convencer de que a Equação I é razoável. f x = x 2 , a = 0 ,b = 1 e c = 1 .