Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.10 - Ex. 43
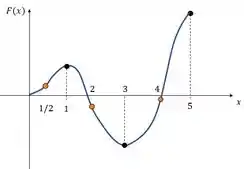
Seja , onde é a função cujo gráfico é mostrado abaixo.
(a) Onde ocorrem os mínimos relativos de ?
(b) Onde ocorrem os máximos relativos de ?
(c) No intervalo , onde ocorre o máximo absoluto de ?
(d) No intervalo onde ocorre o mínimo absoluto de ?
(e) Onde é côncava para cima e onde é côncava para baixo?
(f) Esboce o gráfico de .
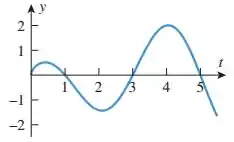
Passo 1
(a) Para achar os mínimos relativos de , precisamos descobrir a derivada dela.
Podemos usar a parte 2 do teorema fundamental do cálculo para achar a derivada:
Vemos que a derivada de é a própria função . Logo, podemos tirar todas informações sobre ela do gráfico.
Por isso, o mínimo relativo de vai ocorrer no ponto:
Porque nele:
E antes dele a derivada tem valores negativos e depois a derivada tem valores positivos. Esse é o teste da derivada primeira.
Passo 2
(b) Pelo teste da derivada primeira, os máximos relativos de vão ocorrer onde tem valores positivos antes do ponto, onde , e negativos depois do ponto.
Isso ocorre em:
Passo 3
(c) O máximo absoluto vai ocorrer em um dos extremos do intervalo ou em um dos máximos relativos.
Vamos escolher o ponto:
Porque antes dele a função , que é a nossa derivada, tem o intervalo onde há a maior área positiva. Isso quer dizer que antes desse ponto, a função cresceu mais do que em outro momento.
Por isso, esse é o ponto mais alto do gráfico de .
Passo 4
(d) O máximo absoluto vai ocorrer em um dos extremos do intervalo ou em um dos mínimos relativos.
Vamos escolher o ponto:
Porque antes dele a função , que é a nossa derivada, tem o intervalo onde há a maior área negativa. Isso quer dizer que antes desse ponto, a função decresceu mais do que em outro momento.
Por isso, esse é o ponto mais baixo do gráfico de .
Passo 5
(e) Vemos a concavidade pelo sinal da segunda derivada, e fazer isso é o mesmo que olhar os intervalos de crescimento e decrescimento de . Já que:
Vemos que a função cresce nos intervalos:
Isso quer dizer que neles, e a concavidade nesses intervalos está voltada para cima.
Vemos que a função decresce nos intervalos:
Isso quer dizer que neles, e a concavidade nesses intervalos está voltada para baixo.
Passo 6
(f) Para fazer o esboço, é só colocar as informações que a gente reuniu em um gráfico. Fica assim:
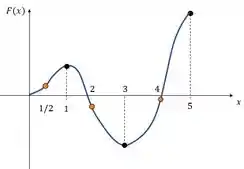
Resposta
- ,
- Concavidade para cima: , Concavidade para baixo:
