Os programas CAS têm comandos para trabalhar com a maioria das funções não elementares importantes. Verifique seu manual para informações sobre a função erro [veja a Fórmula (12)] e, então, faça o seguinte.
(a) Gere o gráfico de
(b) Use o gráfico para fazer uma conjectura sobre a existência e a localização de possíveis máximos e mínimos relativos de
(c) Verifique sua conjectura em (b) usando a derivada de
(d) Use o gráfico para fazer uma conjectura sobre a existência e a localização de possíveis pontos de inflexão de
(e) Verifique sua conjectura em (d) usando a derivada segunda de
(f) Use o gráfico para fazer uma conjectura sobre a existência de assíntotas horizontais de
(g) Verifique sua conjectura em (f) usando o CAS para encontrar os limites de quando .
Passo 1
(a) Vamos usar a calculadora CAS do Geogebra (dá para acessar pelo navegador) para fazer esse gráfico:
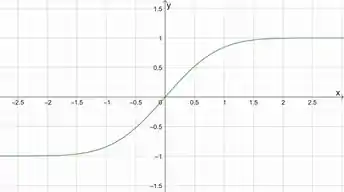
Passo 2
(b) Olhando o gráfico, não conseguimos identificar nenhum ponto onde há algo parecido com um morro ou um vale.
Por isso a gente pode dizer que não visualizou nenhum ponto de máximo ou mínimo relativo.
Passo 3
(c) A função tem essa cara:
Usamos a parte 2 do teorema fundamental do cálculo para achar a derivada dela:
Os máximos e mínimos relativos de uma função ocorrem em . Mas repara que a derivada de nunca chega a ser igual a zero, por ser um exponencial natural.
Assim, não há realmente máximos e mínimos relativos.
Passo 4
(d) O ponto de inflexão é onde o gráfico muda de concavidade, e isso acontece, visualmente, só em .
Passo 5
(e) Os pontos de inflexão acontecem em . Vamos calcular a derivada segunda de pela regra da cadeia:
Vemos que essa derivada segunda só zera em , logo esse é o único ponto de inflexão mesmo. 😊
Passo 6
(f) Vemos que o gráfico se aproxima muito de e , mas não chega a passar por esses pontos. Então podemos esperar que essas são assíntotas horizontais para .
Passo 7
(g) Usando a calculadora CAS do Geogebra, vemos que:
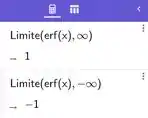
Isso confirma para gente a existência de assíntotas em e .
Resposta
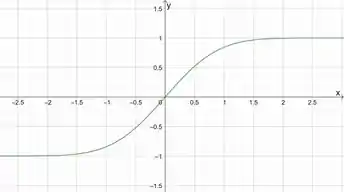
- (c) Não há máximos e mínimos relativos.
- (e) O ponto de inflexão ocorre em .
(f) (g) As assíntotas ocorrem .