Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 35
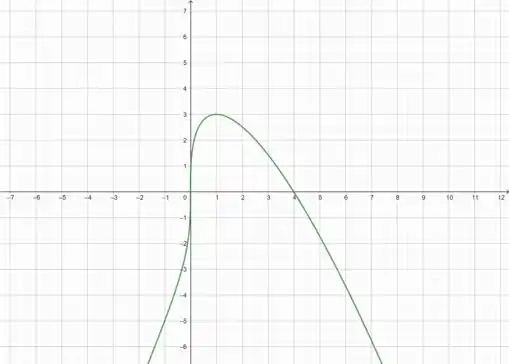
Obtenha um gráfico da função e identifique a localização de todos os pontos criticos e de inflexão. Confira seu trabalho com um recurso gráfico.
35.
Passo 1
Vamos começar com os pontos críticos, que calculamos fazendo a derivada e igualando ela a zero ou no ponto indefinido.
Então vamos fazer a derivada de
Os pontos críticos são onde é igual a zero ou indefinido, neste caso
, e
Agora para achar o ponto de inflexão vamos derivar
Vamos ter os pontos de inflexão quando:
Passo 2
Nosso gráfico então fica:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
determine a derivada usando a definição de f t = 1 2 t + 1
Para qual (quais) valor( es) da constante m, se houver, a função, f x = { s e n 2 x,x ≤ 0 m x ,0x é contínua em x=0 ?é derivável em x=0 ?
determine a derivada usando a definição de g x =2 x 2 + 1
Trace o gráfico da função f x = { x,- 1 ≤ x0 t g x ,0 ≤ x ≤ π / 4 f é contínua em x=0 ? f é derivável em x=0 ?