Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.6 - Ex. 2
Seja para e seja
(a) Encontre os coeficientes na expansão de em termos de .
(b) Calcule o erro médio quadrático para diversos valores de e faça um gráfico dos
resultados.
(c) Encontre o menor valor de para o qual
Passo 1
Utilizando para
a)
E este é nosso coeficiente, aplicando a integral, por método por partes, temos:
E
Substituindo:
Retomando as constantes e aplicando o intervalo de integração, ficamos:
Aplicando a soma parcial temos:
Passo 2
b) bem vamos ao calculo sequencial, utilizando Excel, temos:
Calculando de e após isto passos de 5 a 5 até 25.
E para isto teremos os seguintes
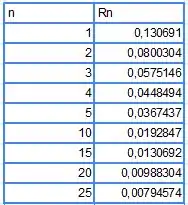
Agora desenhando o gráfico dos valores temos,
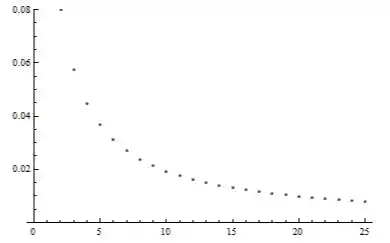
Passo 3
c)Utilizando a tabela que acabamos de calcular, é fácil de identificar o menor valor de que corresponde para , com .
Resposta
a)
c), para
Exercícios de Livros Relacionados
Suponha que todos os autovalores são reais.Determine a forma das autofunções e a equação satisfeita pelos autovalores não nulos.
Suponha que todos os autovalores são reais.Encontre valores aproximados para λ1 e λ2, os dois autovalores não nulos de menor módulo.
Considere o problema.Mostre que, se φm e φn são autofunções associadas aos autovalores λm e λn, respectivamente, com λm ≠ λn, então
Considere o problema de valores de contorno. Resolva também o problema dado diretamente (sem introduzir uma variável nova).
Determine se o problema de valores de contorno dado é autoadjunto.