Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 36
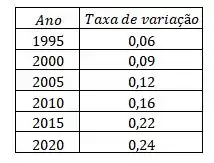
Seja a porcentagem da população das Filipinas com idade maior que 60 anos no instante . A tabela fornece projeções dos valores desta função de 1995 a 2020.
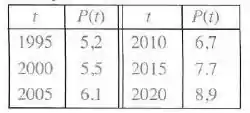
- Qual o significado de ? Quais são as suas unidades?
- Construa uma tabela de valores para
- Faça os gráficos de e
Passo 1
E aí! como vai?
Nesse problema foi dada a tabela
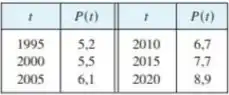
Onde é função porcentagem da população das Filipinas que tem idade maior que anos e é o ano.
A partir dessa tabela, queremos saber qual o significado de e suas unidades, constuir uma tabela de e esboçar os gráficos de e .
Tem ideia de como fazemos isso?
Primeiramente temos que lembrar de algumas propriedades de definição de derivadas... em um ponto, a derivada de uma função é igual a inclinação da reta tangente a essa função naquele ponto.
Para obter a tabela de temos que aplicar a formilinha
E para esboçar os gráficos, plotamos os pontos da tabela no plano cartesiano e ligamos eles imaginando o comportamento da função.
Sacou? Bora começar!
Passo 2
Vamos começar definido o que é ...
Extendendo o que foi dito no passo 1, é a taxa na qual a porcentagem da população das Filipinas com idade maior que 60 anos está mudando em relação ao tempo. Isso porque se a derivada de uma função é a inclinação da função em um determinado ponto, podemos interpretar a derivada nesse caso como uma variação instantânea de ...
Como é o quando a porcentagem muda em relação ao tempo, suas unidades são porcentagem por ano
Tranquilo até aqui?
Passo 3
Agora vamos construir a tabela de
Podemos encontrar o valor da derivada fazendo
Como estamos lidando com uma tabela e não com uma função em tempo contínuo, podemos dizer que
Dessa forma, para 1995
A partir desse ponto, vamos calcular a derivada a partir das medias das derivadas laterais...
Para 2000, primeiro calculamos de para
Agora de para
Calculando a media entre esses dois valores...
Vamos fazer a mesma coisa para 2005...
Enter e
Entre e
Calculando a média...
Repetindo o processo para todos os anos, podemos montar a tabela
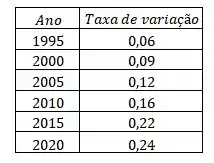
Show?
Passo 4
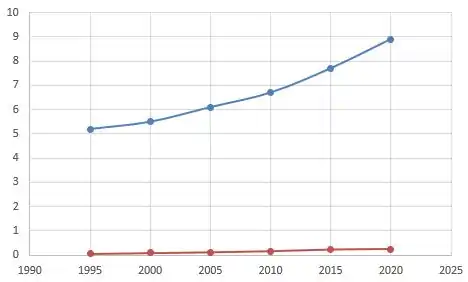
Por fim, plotando os pontos de e no plano cartesiano e ligando-os, podemos esboçar seus gráficos como
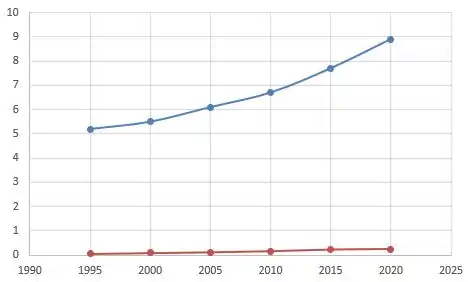
Onde a linha em azul representa e a linha vermelha
E aí! entendeu tudo? Responde Aí!
Resposta
- é a taxa na qual a porcentagem da população das Filipinas com idade maior que 60 anos está mudando em relação ao tempo. Suas unidades são porcentagem por ano
-
