Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 3.7 - Ex. 3

Uma partícula se move com s = f t ,   t ≥ 0 :

f t = s e n π t 2

  1. Encontre a velocidade
  2. Encontre a velocidade para t = 1
  3. Quando a partícula está em repouso?
  4. Quando a particula se move na direção positiva?
  5. Qual a distância percorrida em 6 segundos?
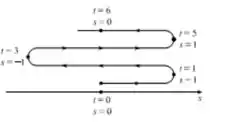
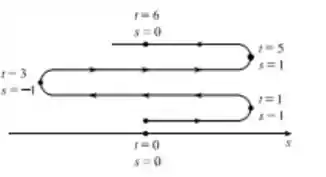
  6. Desenhe o diagrama que mostre a movimentação da partícula
  7. Ache a função da aceleração e depois a aceleração depois de 1 segundo
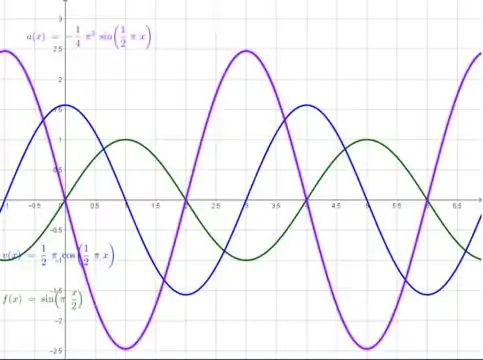
  8. Faça o gráfico da velocidade, posição e aceleração
  9. Quando a partícula está acelerando? E desacelerando?

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui temos a equação do espaço do movimento, e a partir do uso da derivação iremos encontrar as equações da velocidade e da aceleração.

Passo 2

  1. A velocidade é a derivada da posição:

    2. f ' t = π 2 cos ⁡ π t 2

  2. Basta substituir o t por 1:

    3. f ' 1 = π 2 cos ⁡ π 2 = 0

  3. Basta igualar o f ' ( t )   a 0, pois em repouso a velocidade será zero:

    4. π 2 cos �� π t 2 = 0

    cos ⁡ t π 2 = cos ⁡ π 2

    A partícula está em repouso quando:

    π t 2 = π 2 + 2 π n

    t = 1 + 4 n

    Sendo n inteiro.

  4. A partícula está se movendo na direção positiva quando a velocidade é positiva e, portanto, exigimos  v ( t ) > 0 .

    5. Utilizaremos o fato de que cos ⁡ x > 0   quando π ( 4 k - 1 ) 2 < x < π ( 4 k + 1 ) 2

    v t > 0

    π 2 cos ⁡ π t 2 > 0

    cos ⁡ π t 2 > 0

    π ( 4 k - 1 ) 2 < π t 2 < π ( 4 k + 1 ) 2

    4 k - 1 < t < 4 k + 1

    0 ≤ t < 1 e 4 k - 1 < t < 4 k + 1

    Assim, a velocidade é positiva quando  0 ≤ t < 1  e  4 k - 1 < t < 4 k + 1  para todos os inteiros positivos de k.

  5. Por ser a distância TOTAL, isso significa que quando a partícula se move para trás, a distância continua a aumentar enquanto sua posição flutua. Isso significa que enquanto  0 < f ' ( t )  ou  f ' ( t ) < 0 , precisamos resumir a mudança total entre dois pontos  ∣ △ F ( x ) ∣

    6. Não basta aplicar 6 na equação da posição, pois a equação muda de sinal, logo:

    f 1 - f 0 + f 3 - f 1 + f 5 - f 3 + f 6 - f ( 5 ) = 6

    Passo 3

  6. Vamos determinar a posição inicial, a posição final e a posição em que a partícula muda de direção:

    s 0 = f 0 = sin ⁡ π 0 2 = sin ⁡ 0 = 0

    s 1 = f 1 = sin ⁡ π 1 2 = sin ⁡ π 2 = 1

    s 3 = f 3 = sin ⁡ π 3 2 = sin ⁡ 3 π 2 = 1

    s 5 = f 5 = sin ⁡ π 5 2 = sin ⁡ 5 π 2 = 1

    s 7 = f 7 = sin ⁡ π 7 2 = sin ⁡ 7 π 2 = - 1

    A partícula então se move de posição s = 0  para posicionar  s = 1  durante o primeiro segundo, então a partícula se move de volta à posição  s = - 1  Durante os dois segundos seguintes, as partículas voltam à posição  s = 1  durante os próximos dois segundos, e assim por diante.

  7. Basta derivar a velocidade e substituir o valor:

    8. f ' ' t = - π 2 4 s e n π t 2

    f ' ' 1 = - π 2 4

  9. A partícula esta acelerando quando a aceleração e a velocidade estão na mesma direção. Ou seja, quando a aceleração e a velocidade são negativas ou ambas positivas.

v t > 0

π 2 cos ⁡ π t 2 > 0

cos ⁡ π t 2 > 0

π 2 4 k - 1 < π t 2 < π 2 4 k + 1

4 k - 1 < t < 4 k + 1

0 ≤ t < 1 e 4 k - 1 < t < 4 k + 1

Podemos então concluir que a velocidade é positiva quando ( 0   ≤ t   <   1 ) e ( 4 k - 1   <   t   <   4 k + 1 ) para todos os inteiros positivos ( k ) , enquanto a velocidade é negativa quando ( 4 k - 3   <   t   <   4 k - 1 ) para todos os inteiros positivos ( k ) .

Resposta

  1. f ' t = π 2 cos ⁡ π t 2
  2. f ' 1 = π 2 cos ⁡ π 2 = 0
  3. t = 1 + 2 n ,   n   i n t e i r o
  4. Temos que ver o intervalo onde a velocidade é positiva. Sabemos que o cosseno será positivo quando 0 < t < 1,3 < t < 5,7 < t < 9 .
  5. Não basta aplicar 6 na equação da posição, pois a equação muda de sinal, logo:

    6. f 1 - f 0 + f 3 - f 1 + f 5 - f 3 + f 6 - f ( 5 ) = 6

  7. f ' ' t = - π 2 4 s e n π t 2 ; f ' ' 1 = - π 2 4
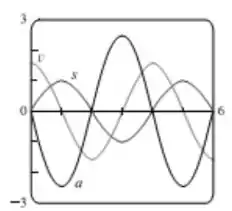
  9. Logo, está acelerando quando   1 < t < 2,3 < t < 4 e desacelerando quando 0 < t < 1,2 < t < 3   e   4 < t < 5 . .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o roteiro desta seção para esboçar a curva. y = ln ⁡ x x 2
Use o roteiro desta seção para esboçar a curva.y = x e^(- x^2)
Use o roteiro desta seção para esboçar a curva. y = e x x
Use o roteiro desta seção para esboçar a curva. y = ln ⁡ ( s e nx ) 2
Use o roteiro desta seção para esboçar a curva. y = x - ln ⁡ x