Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.3 - Ex. 48
48. Seja
- Determine cada um dos seguintes limites ou explique por que ele não existe.
- Para quais valores de a o limite não existe?
- Esboçe o gráfico de .
Passo 1
Muito bom galerinha, primeiro de tudo aqui, a gente quer informações da função , só que essa função é meio diferente do normal, ela define valores fixos de acordo com o domínio. Mas calma lá chefia, que a coisa não tá tão feia assim, se liga só, a função é definida por
Só que a malandragem aqui é que o domínio está restrito aos valores de , e na nossa função o domínio está definido por outra função, já que a função é , portanto podemos expressar a função como:
Mó legal né?! HUEHEUE agora que a gente já tem a função definida, podemos analisar os limites, bora lá.
Passo 2
Belezoca galera, dado que a função é
Na letra (a) vamos analisar cada limite individualmente.
Quando o tende a pela direita, isto é, com temos valores maiores do que , o que nos retorna
E de acordo com a função que definimos, temos então
Agora, estamos com tendendo a zero pela esquerda, com temos valores menores do que , daí a gente tira que
E de acordo com , temos que
Agora, queremos ver como a fun�o se comporta quando o limite tende , dessa forma temos , o que retorna pra gente que
E ai a gente vai lá na função e olha a respot...ERRADO!!! Não podemos de maneira alguma cair nessa tentação, a definição de limite exige que os limites laterais tendendo pela direita e pela esquerda do ponto coincidam, isto é, para que o limite da função quando tende a exista é obrigatório que:
Mas como vimos em (i) e em (ii), temos que e . Logo, eles não coincidem e por este motivo o limite não existe.
Agora, o limite é para , temos então que:
E a fun��ão retorna pra gente que:
E aqui galerinha, temos o mesmo ponto, só que agora ele tende a pela esquerda,
E retorna pra gente que
Novamente, os limites laterais de (iv) e de (v) divergem, fazendo com que o nosso limite não exista.
Passo 3
Na letra (b), os valores para os quais o limite não existe, são justamente aqueles em que a função troca de sinal, isto é, nos ponto em que a função troca de negativa para positiva e vice versa. Pra ficar mais bonitinho, a gente pode falar que esses pontos são todos os valores de quando
Podemos escrever esses valores da seguinte forma
Passo 4
E agora o gráfico, como a função é uma função periódica, a função tem toda a cara de que será também, então dado
Pegando valor a valor, podemos traçar o gráfico que fica como
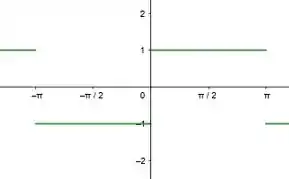
Agora ficou maneiro heim meu patrão.
Resposta
-
(i)
(ii)
(iii)
(iv)
(v)
(vi)
