Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano . Calcular
Onde
- S é a face da frente de T
- S é a face de T que esta no plano xz
- S é face de T que esta no plano yz
- S é face de T que esta no plano xy
- Some os resultados dos itens acima e interprete fisicamente
Passo 1
Estamos trabalhando com varias superfícies aqui. Temos todos os planos coordenados e esse plano . Que podemos ver abaixo
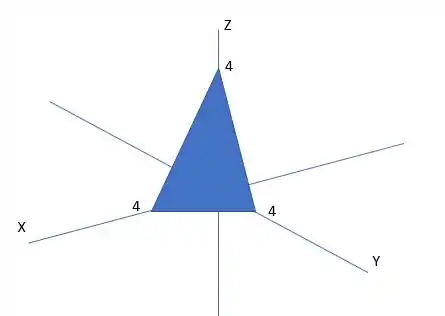
Passo 2
- S é a face da frente de T
Nossa função é
E nossa superfície é
Nossa integral tem a seguinte estrutura
E se conseguirmos projetar essa superfície me algum dos planos coordenados – por exemplo o XY – temos que
Passo 3
Vamos calcular nossa função normal
Sabemos que
Logo calcular o gradiente de g não é tao complicado. ( Pra quem ainda se perde um pouco é o operador Gradiente e tem a seguinte forma , logo obtemos um vetor quando aplicamos o gradiente. Agora o operador Se chama Divergente e tem a seguinte forma OU seja fazemos um produto de vetores o que nos retorna um escalar. Isso é importante porque o significado Físico de Gradiente e Divergente são completamente diferente. Gradiente é o vetor de incremento da nossa superfície, ou função. Já Divergente está ligado a fluxo – Fontes ou Sumidouros de Campos Vetoriais. Pensando em fluidos – o gradiente diria a direção para onde um rio está correndo, o divergente diria onde está a nascente do rio )
Assim o modulo do gradiente é
Vamos retornar a nossa integração
Vamos projetar z no plano XY
Agora vamos escolher nossos intervalos de integração
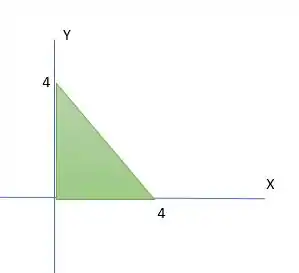
Para escolher os intervalos de integração basta olhar para o gráfico
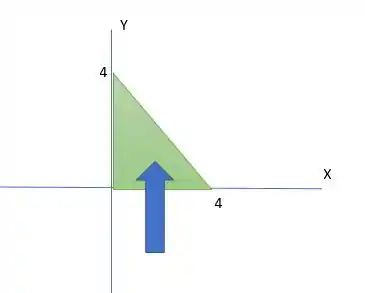
Se olharmos para o eixo y de baixo para cima. Nossa superfície começa em e sempre para na reta . Assim nosso intervalo de integração é esse
E para x nos reta um intervalo numérico
Agora é apenas trabalho braçal de integrar
Terminamos por aqui. Te vejo na próxima resolução
: )