Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 16.7 - Ex. 23

Calcule a integral de superfície ∫ ∫ S   F ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação positiva (para fora).

F x ,   y ,   z = x   i + y   j + z   k   ,

S é a esfera x 2 + y 2 + z 2 = 9 .

Passo 1

E aiii meu povo, belezinha!? Bora lá então!

Precisamos calcular o fluxo de F através da superfície S.

∫ ∫ S   F ∙ d S

Onde,

F x ,   y ,   z = x   i + y   j + z   k   ,

E S é a esfera x 2 + y 2 + z 2 = 9 .

Observe que nossa superfície é uma esfera, certo? Nesse tipo de situação devemos trabalhar com coordenadas esféricas:

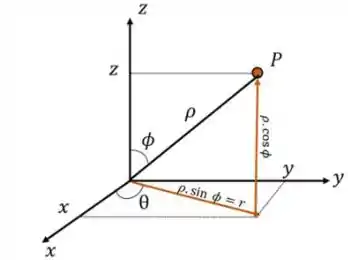
Onde,

  0 ≤ ϕ ≤ π   ,     0 ≤ θ ≤ 2 π

Como estamos determinando o fluxo, que é uma integral dupla, vamos manter o raio da esfera fixo 3 .

Sabendo disso, podemos escrever uma parametrização em função dos ângulos r ϕ ,   θ da seguinte forma:

r ϕ ,   θ = 3   s e n   ϕ cos ⁡ θ i + 3   s e n   ϕ   s e n   θ   j + 3 cos ⁡ ϕ   ,     0 ≤ ϕ ≤ π   ,     0 ≤ θ ≤ 2 π

Aqui vamos usar uma outra relação da integral de superfície, a seguinte:

∫ ∫ S   F ∙ d S = ∫ ∫ D F ( r ϕ ,   θ ) ∙ r ϕ × r θ d A

Nossa missão é, parametrizar o campo F ( r ϕ ,   θ ) e calcular o produto vetorial r ϕ × r θ , onde r ϕ representa a derivada de r   em relação a ϕ e r θ é a derivada de r em relação a θ .

Depois é só fazer o produto escalar e resolver a integral.

Vamos nessa!

Passo 2

Vimos que a parametrização para esfera é:

r ϕ ,   θ = 3   s e n   ϕ cos ⁡ θ i + 3   s e n   ϕ   s e n   θ   j + 3 cos ⁡ ϕ

Vamos começar determinando as derivadas r ϕ e r θ .

Temos que r ϕ representa a derivada de r   em relação a ϕ . Derivando, obtemos:

r ϕ = 3 cos ⁡ ϕ cos ⁡ θ i + 3 cos ⁡ ϕ s e n   θ   j - 3   s e n   ϕ   k

E r θ é a derivada de r em relação a θ . Derivando, vamos ter:

r θ = - 3   s e n   ϕ   s e n   θ   i + 3   s e n   ϕ cos ⁡ θ j + 0   k

Pronto, agora vamos determinar o produto vetorial:

r ϕ × r θ

Pois precisamos para substituir na integral.

∫ ∫ D F ( r ϕ ,   θ ) ∙ r ϕ × r θ d A

Vamos escrever esse produto vetorial na forma matricial. Desse jeito:

r ϕ × r θ = i j k 3 cos ⁡ ϕ cos ⁡ θ 3 cos ⁡ ϕ s e n   θ - 3   s e n   ϕ - 3   s e n   ϕ   s e n   θ 3   s e n   ϕ cos ⁡ θ 0

Aplicando o determinante, vamos obter como resposta:

r ϕ × r θ = 9   s e n 2   ϕ cos ⁡ θ i + 9   s e n 2   ϕ   s e n   θ   j + 9   s e n   ϕ cos ⁡ ϕ k

Agora, vamos parametrizar o campo F r ϕ ,   θ . Substituindo pela parametrização, temos:

F r ϕ ,   θ = 3   s e n   ϕ cos ⁡ θ i + 3   s e n   ϕ   s e n   θ   j + 3 cos ⁡ ϕ k

Passo 3

Agora, lembre-se que:

∫ ∫ S   F ∙ d S = ∫ ∫ D F ∙ r u × r v d A

Sabemos que os intervalos de integração são:

0 ≤ ϕ ≤ π   ,     0 ≤ θ ≤ 2 π

Assim, a integral fica:

∫ 0 2 π ∫ 0 π ( 3   s e n   ϕ cos ⁡ θ , 3   s e n   ϕ   s e n   θ , 3 cos ⁡ ϕ ) . 9   s e n 2   ϕ cos ⁡ θ ,   9   s e n 2   ϕ   s e n   θ , 9   s e n   ϕ cos ⁡ ϕ k     d ϕ   d θ

Fazendo o produto escalar e simplificando, obtemos:

27 ∫ 0 2 π ∫ 0 π s e n 3   ϕ cos 2 ⁡ θ + s e n 3   ϕ   s e n 2   θ + s e n   ϕ cos 2 ⁡ ϕ   d ϕ   d θ

27 ∫ 0 2 π ∫ 0 π s e n 3   ϕ + s e n   ϕ cos 2 ⁡ ϕ   d ϕ   d θ

27 ∫ 0 2 π ∫ 0 π s e n   ϕ   d ϕ   d θ

Observe que até então, só fomos simplificando. Utilizando a relação trigonometria s e n 2   ϕ + cos 2 ⁡ ϕ = 1 .

Agora vamos começar a integrar. Integrando em relação d ϕ , vamos ter:

27 ∫ 0 2 π - cos ⁡ ϕ 0 π   d θ

Aplicando os limites, temos:

27 ∫ 0 2 π - cos ⁡ π + cos ⁡ 0   d θ

27 ∫ 0 2 π - ( - 1 ) + 1   d θ

54 ∫ 0 2 π d θ  

Integrando por fim em relação a d θ , vamos ficar com:

54 ( θ ) 0 2 π  

Aplicando os limites de integração, temos:

54 2 π

Logo, nossa resposta é:

∫ ∫ S   F ∙ d S = 108 π

Resposta

∫ ∫ S   F ∙ d S = 108 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral de superfície ∬ F . d S para o campo vetorial F e a superfície S . Em outras palavras, localize o fluxo de F através de S . Para superfícies fechadas, use a orientação (para o exteri
Avalie a integral de superfície ∬ S F → ⋅ d S → para o campo vetorial dado F → e a superfície orientada S . Em outras palavras, localize o fluxo de F através deS . Para superfícies fechadas, use a ori
Avalie a integral de superfície ∬ F ⋅ d S para o campo vetorial F e a superfície S . Em outras palavras, localize o fluxo de F através de S . Para superfícies fechadas, use a orientação (para o exteri
Calcule ∬ S x 2 + y 2 + z 2 d S com precisão de quatro casas decimais, quando S é a superfície z = x e y , 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 .
Determine o valor exato de ∬ S x 2 y zd S , onde S é a superfície z = x y , 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 .