Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 31
31. Seja T(t) a temperatura (em °F) em Dallas horas após a meia-noite em 2 de junho de 2001. A tabela mostra os valores dessa função registrados de duas em duas horas. Qual o significado de ? Estime o seu valor.
Passo 1
Olá, meu colega. Tudo bem com você? Espero que sim, pois vamos dar início a mais uma resolução aqui, com o padrão de qualidade que você já conhece.
Veja bem, a questão nos apresenta uma tabela de temperatura em em função do tempo, e nos pergunta o significado da derivada da temperatura em relação ao tempo, no tempo .
Inicialmente, devemos lembrar que a derivada pode ser interpretada como uma taxa de variação e você deve ter percebido que é essa definição que usaremos nesses problemas.
Passo 2
é taxa de variação da temperatura, com relação ao tempo após a meio noite (, no nosso problema é quando horas após a meia noite.
Passo 3
Agora faremos uma nova tabela com os valores da seguinte expressão:
E será os valores registrados na tabela do enunciado, porém calmaa! O não iremos calcular, pois se calculássemos teríamos no denominador.
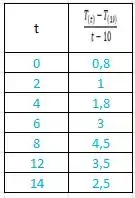
O está entre os valores de e e vamos assumir que não tenha nenhuma mudança brusca nos valores entre e .Iremos fazer a média aritmética simples entre os valores de temperatura.
Não esqueça das unidades hein! Taxa tem um significado teórico, no nosso caso é a variação da temperatura dividido por .
Resposta
é taxa de variação da temperatura, com relação ao tempo após a meio noite (, no nosso problema é quando horas após a meia noite,