Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.8 - Ex. 9

9.(a) Se F ( x ) = x 3 - 5 x + 1 , encontre F ' ( 1 ) e use-o para achar uma equação da reta tangente à curva y = x 3 - 5 x + 1 no ponto ( 1 , - 3 )

(b) Ilustre a parte (a) fazendo o gráfico da curva e a reta tangente na mesma tela.

Passo 1

Olá, querido amigo. Vamos resolver mais uma atividade.

Aqui a gente precisa encontrar a derivada da função dada

F ( x ) = x 3 - 5 x + 1

e a equação da reta tangente a esta curva e que passa no ponto ( 1 , - 3 ) .

Para calcularmos   F ' ( 1 ) iremos utilizar a fórmula abaixo:

F ' ( 1 ) = lim h → 0 ⁡ F ( 1 + h ) - F ( 1 ) h

Já a equação da reta tangente é dada por:

y - y 0 = F ' ( 1 ) ( x - x 0 )

Onde ( x 0 , y 0 ) são os pontos pelos quais a reta deve passar, no nosso caso:

y - - 3 = F ' ( 1 ) ( x - 1 )

Passo 2

Letra a)

Agora que já colocamos as fórmulas no passo anterior, temos que fazer os cálculos dessa situação, vamos com atenção para não errar.

Inicialmente, vou anotar algumas coisas:

F ( x ) = x 3 - 5 x + 1

F 1 + h = 1 + h 3 - 5 1 + h + 1

Realizando o produto notável:

F 1 + h = 1 + 3 h + 3 h 2 + h 3 - 5 - 5 h + 1

Simplificando os termos semelhantes:

F 1 + h = h 3 + 3 h 2 - 2 h - 3

Agora para x = 1 :

F 1 = 1 3 - 5 1 + 1 = 1

Colocando tudo na expressão do limite, vamos ter:

F ' 1 = lim h → 0 ⁡ h 3 + 3 h 2 - 2 h - 3 - - 3 h

F ' 1 = l i m h → 0 h 3 + 3 h 2 - 2 h - 3 + 3 h

F ' 1 = l i m h → 0 h 3 + 3 h 2 - 2 h h

Vamos simplificar o h da parte de cima com o h da parte de baixo:

F ' ( 1 ) = l i m h → 0 ( h 2 + 3 h - 2 ) = - 2

Passo 3

Voltando para resolvermos o problema da equação da reta tangente, vai ser mais uma substituição de variáveis. Dessa forma olho no lanceee!

y - y 0 = F ' ( 1 ) ( x - x 0 )

y - ( - 3 ) = - 2 ( x - 1 )

y + 3 = - 2 x + 2

y = - 2 x - 1

Passo 4

Letra b)

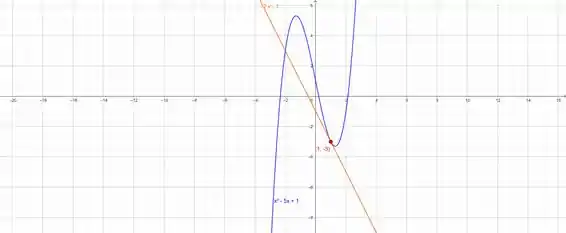
Agora vamos ao gráfico. Aqui irei ter ajuda do GeoGebra, fique à vontade para gerar o gráfico no seu software favorito.

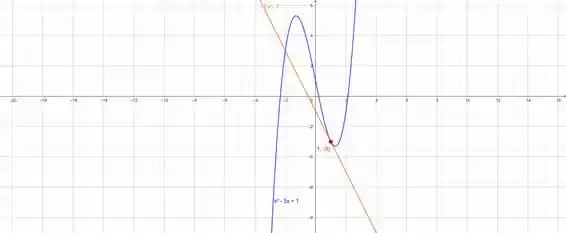
Podemos ver então que acertamos. Um forte abraço e até a próxima.

Resposta

(a)

F ' ( 1 ) = - 2

y = - 2 x - 1

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para quais valores de a e b a reta 2 x + y = b é tangente à parábola y = a x 2 quando x = 2 ?
Encontre uma função cúbica cujo gráfico y = a x 3 + b x 2 + c x + d tenha tangentes horizontais nos pontos - 2,6 e 2,0 .
Uma reta tangente à hipérbole x y = c é traçada em um ponto P .a) Mostre que o ponto médio do segmento de reta cortado dessa reta tangente pelos eixos coordenados é P .b) Mostre que o triangulo formad