Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 1a
1. Determinar a equação da reta tangente às seguintes curvas, nos pontos indicados. Esboçar o gráfico em cada caso.
(a)
Passo 1
Podemos calcular o coeficiente angular de uma reta tangente usando a definição da derivada de uma função, em que o coeficiente da reta tangente é a derivada da função no ponto desejado. Ou seja:
Onde representa o ponto desejado.
Passo 2
Temos que calcular então a derivada da curva . Podemos rescrever a função da seguinte forma:
Calculando a derivada temos:
A derivada de é
Passo 3
Para encontra o coeficiente angular da reta tangente , é só calcularmos .
Temos que para :
Temos então que para a reta tangente no ponto .
Temos que para :
Temos então que para a reta tangente no ponto .
Passo 4
Para encontrarmos a equação de uma reta, precisamos do coeficiente angular e um ponto que onde passa a reta.
Para podemos encontrar esse ponto calculando .
Um ponto por onde a reta tangente passa é .
Para podemos encontrar esse ponto calculando .
Um ponto por onde a reta tangente passa é .
Passo 5
Toda reta pode ser escrita da seguinte forma:
Onde é o coeficiente angular e é o coeficiente linear.
Para , temos que e temos que a reta passa pelo ponto , assim podemos substituir na equação da reta e encontrar .
O coeficiente linear da reta é , assim a equação da reta é:
Para , temos que e temos que a reta passa pelo ponto , assim podemos substituir na equação da reta e encontrar .
O coeficiente linear da reta é , assim a equação da reta é:
Passo 6
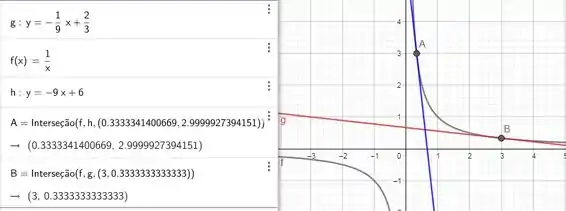
O gráfico da função e das retas tangentes é o seguinte:
Resposta
Para
Para