Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.1 - Ex. 26
Sejam a área entre o gráfico de e o intervalo e a área entre o gráfico de e o intervalo . Explique geometricamente por que .
Passo 1
Bom, o gráfico da função é dado da seguinte maneira:
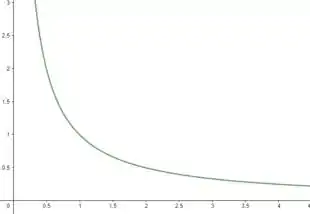
Porém, o problema nos dá os intervalos a serem considerados. Se observarmos através do gráfico os pontos e são espelhos um do outro. Portanto, geometricamente, temos a mesma área com a mesma simetria e iguais.
Resposta
Os pontos são espelhos um do outro e, portanto, iguais.
Exercícios de Livros Relacionados
Nos Exercícios 23-28, use áreas para calcular as integrais.26 ∫ a b 3 td t , 0ab
Nos Exercícios 23-28, use áreas para calcular as integrais.28 f x = 3 x + 1 - x 2 , e ma . - 1,0 eb . [ - 1,1 ]
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.33 ∫ 0 7 3 x 2 d x
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.30 ∫ 0 , 5 2,5 x d x
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.32 ∫ 2 5 2 r d r