69-a)Suponha que um reservatório forneça a água para um parque industrial a uma taxa constante de galões por minuto entre 8h30min e 9h da manhã. Quanta água o reservatório fornecerá durante esse período de tempo ?

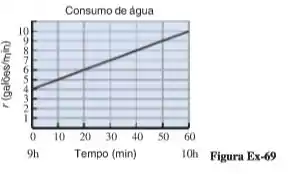
b)Suponha que uma das indústrias aumente seu consumo entre 9h e 10h da manhã e que a taxa segundo o qual o reservatório fornece água cresça linearmente, conforme a figura abaixo. Quanta água o reservatório fornecerá durante aquela 1 hora ?

c)Suponha que, das 10h até as 12h da manhã, a taxa segundo a qual o reservatório fornece água seja dada pela fórmula galões por minuto, onde corresponde às 10h da manhã. Quanta água aquele reservatório fornecerá durante o período de 2 horas?

b)Amiguíneos essa também é muito fácil, só precisamos determinar a área da figura obtida entre o eixo e a reta que representa o crescimento linear da taxa do consumo de água. Vejam só... Nós temos um belo trapézio aqui, né?

Calculando a área do trapézio:

c)Aqui temos um item mais rebuscado, né ??? Não só de questões fáceis vivemos nós estudantes (infelizmente ) hahahah.

Cara, nós temos a função da taxa de água fornecida, mas nós precisamos da quantidade de água que o reservatório vai fornecer durante 2 horas, então adivinhem só o que vamos fazer:

INTEGRAR!!!!

Então, bora montar a nossa integral:

Assim,

Dessa forma,