Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 38
Sejam e .
- Escreva as fórmulas para e
- Determine o domínio de cada uma
- Determine a imagem de cada uma
Passo 1
E aí! Pra essa questão precisamos lembrar de funções inversas:
e . Bora lá?
Passo 2
Só que uma condição de existência: o que tá dentro da raiz de índice par nunca pode ser negativo. Então:
A restrição daqui é pra e
Passo 3
(b) Domínio de :
Lembra que ali em cima ? Então, o domínio é
Domínio de :
Lembra que ali em cima ? Olha só a função:
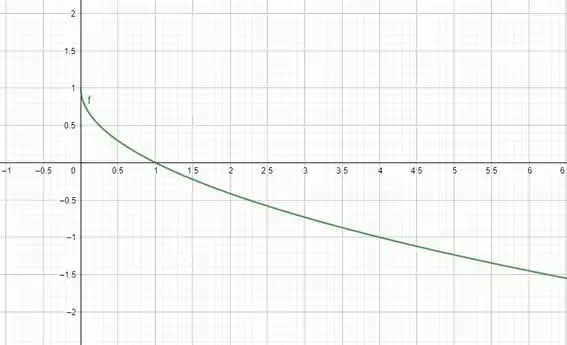
Vale onde tá entre 0 e 1
Então, o domínio é
Passo 4
(c) Olha a cara da :
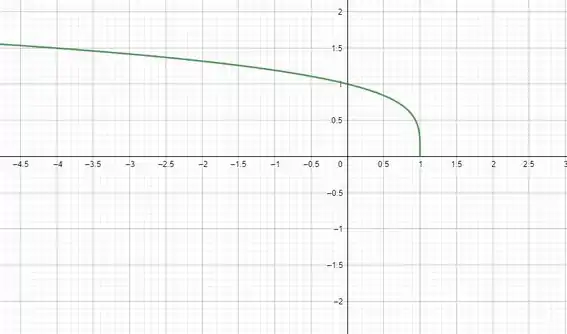
A imagem dela tá de 0 “pra cima”. Então,
E agora olha a cara da (de novo):
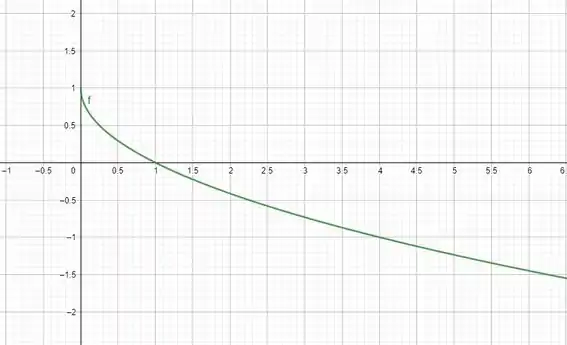
Como ele tá definido só de 0 até 1, a imagem vai de 0 a 1.
Resposta
- ,
- ,
Exercícios de Livros Relacionados
Se f x = x - 1 e g x = 1 / ( x + 1 ) , resolva: f g 1 / 2 g f 1 / 2 f g x g f x f f 2 g g 2 f f x g g x
Se f x = x - 1 e g x = 1 / ( x + 1 ) , resolva: f g 1 / 2 g f 1 / 2 f g x g f x f f 2 g g 2 f f x g g x
Sejam f x = x - 3 , g x = x , h x = x 3 e j x = 2 x . Expressa cada uma das funções como função composta envolvendo uma ou mais funções de f , g , h e j . y = x - 3 y = 2 x y = x 1 / 4 y = 4 x y = x -
Sejam f x = x - 3 , g x = x , h x = x 3 e j x = 2 x . Expressa cada uma das funções como função composta envolvendo uma ou mais funções de f , g , h e j . y = x - 3 y = 2 x y = x 1 / 4 y = 4 x y = x -
Se f x = x + 5 e g x = x 2 - 3 , resolva: f g 0 g f 0 f g x g f x f f - 5 g g 2 f f x g g x