Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 69
Seremos capazes de mostrar, no Capítulo 9 do Volume II, que, sob certas condições, a velocidade de uma gota de chuva caindo no instante é
- Encontre
- Faça o gráfico de v(t) se e . Quanto tempo levará para a velocidade da gota atingir 99% de sua velocidade final?
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui estamos interessandos em calcular o limite da função dada e ainda plotarmos o gráfico dela.
Passo 2
- Calcularemos o limite:
- Substituindo as constantes dadas, ficamos com
vai explodir para valores muito grandes então:
Passo 3
Esboçaremos o gráfico como GeoGebra, que fica
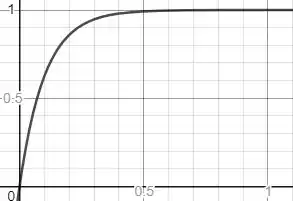
Analisando o gráfico, podemos notar que , ou seja, quando for aproximadamente a velocidade será 99% da sua velocidade final (visto que a velocidade final será de )
Resposta
Exercícios de Livros Relacionados
Calcule o limite e, quando aplicável, indique o teorema de limite usado. lim y → - 4 5 y + 4 y - 5
Calcule o limite e, quando aplicável, indique o teorema de limite usado. lim h → 1 h 2 - 4 3 h 3 + 6
Estabeleça o limite usando a Definição 2.1.1; isto é, para qualquer ϵ 0 , ache umδ 0 tal que se 0x - aδ , então f ( x ) - Lϵ lim x → - 3 4 16 x 2 - 9 4 x + 3 = - 6
Estabeleça o limite usando a Definição 2.1.1; isto é, para qualquer ϵ 0 , ache umδ 0 tal que se 0x - aδ , então f ( x ) - Lϵ lim x → 2 x 2 - 3 x = - 2
Ache o limite, se existir. lim x → 2 + x - 1 x - x ⟦ ⟧ ⟦ ⟧