Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 57
- Se , encontre .
- Verifique se sua resposta em (a) é razoável comparando os gráficos de e .
Passo 1
Olá, vamos resolver essa atividade. Aqui a gente tem a função
Aqui a gente precisa utilizar a regra da cadeia e a regra do produto. Temos o produto entre duas funções, e além disso, a função:
É uma composição de função, temos a função:
E a função:
Bem, vamos então falar agora sobre as regras que iremos utilizar aqui.
Antes de tudo, vamos dar uma olhada na regra da cadeia, ela é utilizada quando devemos derivar uma função composta:
Se e então e a derivada de é:
Agora vamos dar uma olhada também na regra do produto, utilizada quando temos um produto de função:
Dada o produto de função , a regra do produto é:
Passo 2
- Vamos dar uma arrumada na função primeiro:
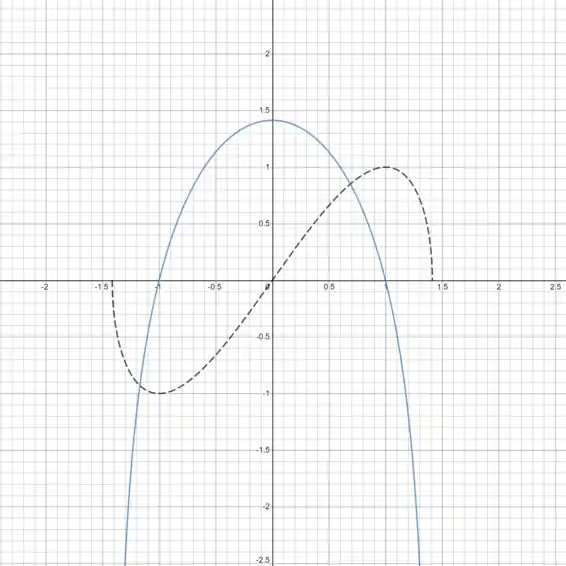
- Temos aqui o gráfico de e :
Aqui vamos usar a regra do produto:
Temos que:
e
Passo 3
Vamos calcular , usando a regra do polinômio:
Passo 4
Vamos agora derivar , usando a regra da cadeia, já que temos a composição de função:
Como consideramos :
Passo 5
Agora é só substituir na expressão:
Agora vamos realizar o para deixar tudo em uma forma mais simplificada possível:
Passo 6
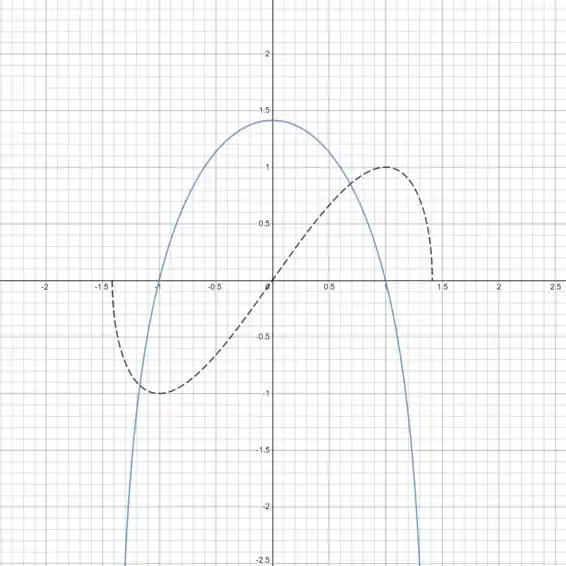
No gráfico abaixo, a curva tracejada preta representa a função e a curva azul representa a derivada .
O gráfico é razoável devido às seguintes observações:
(1) Quando está acima do eixo , a curva preta está aumentando.
(2) Quando está abaixo do eixo , a curva preta está diminuindo.
(3) Quando a curva azul está aumentando, a curva preta está côncava para cima.
(4) Quando a curva azul está diminuindo, a curva preta está côncava para baixo.
(5) A inflexão ocorre na curva preta quando a curva azul tem um máximo local.
(6) Os extremos locais ocorrem na curva preta quando a curva azul intercepta o eixo .
Resposta
a)
b) 